平板のたわみと応力の式
12,491
|
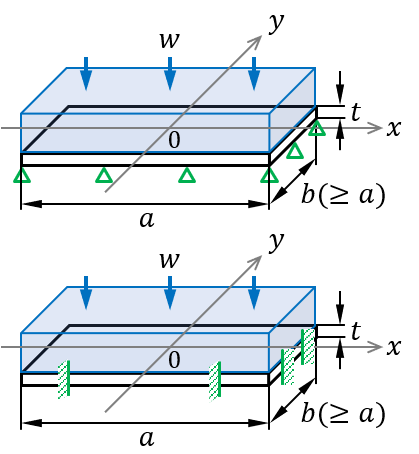
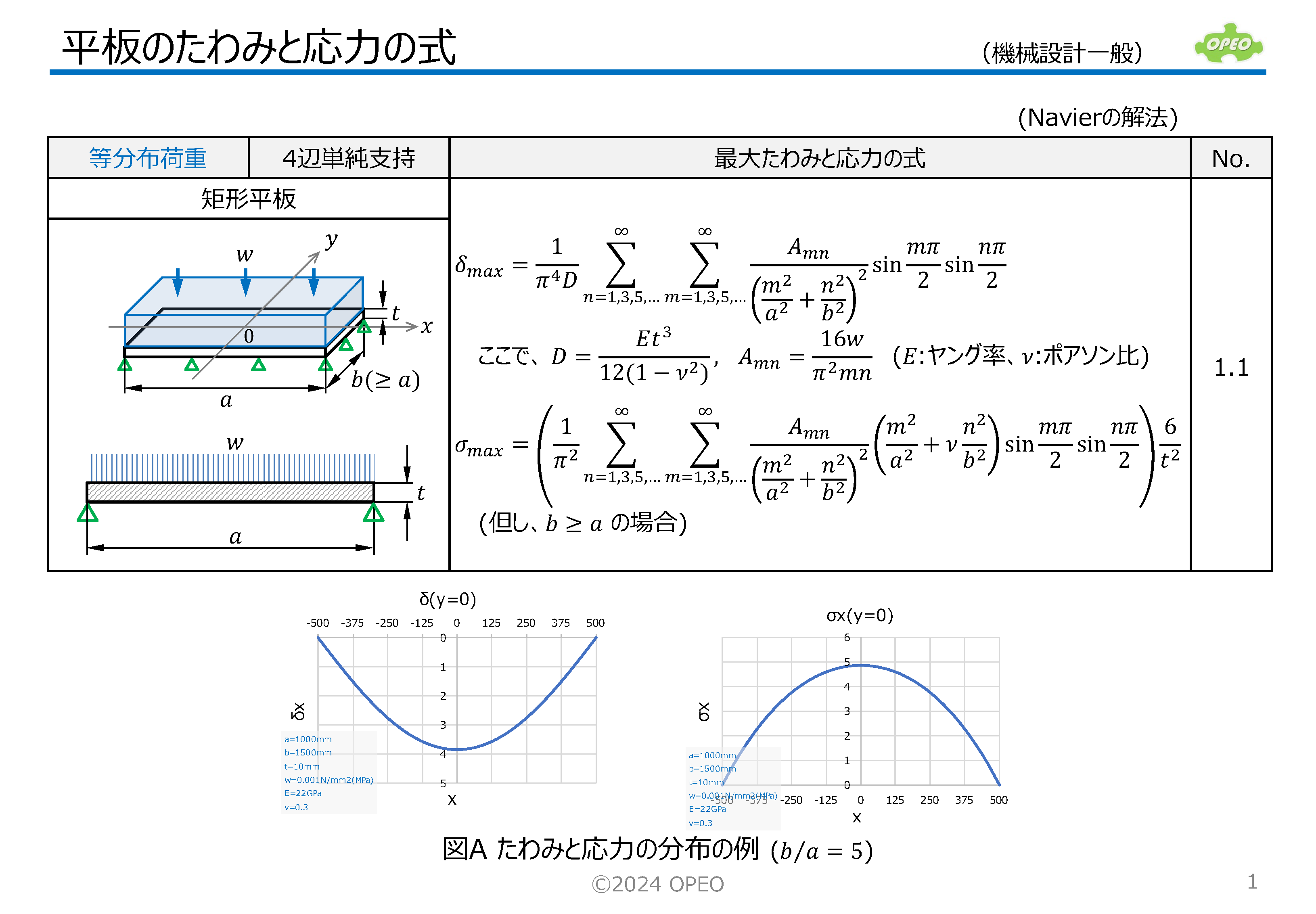
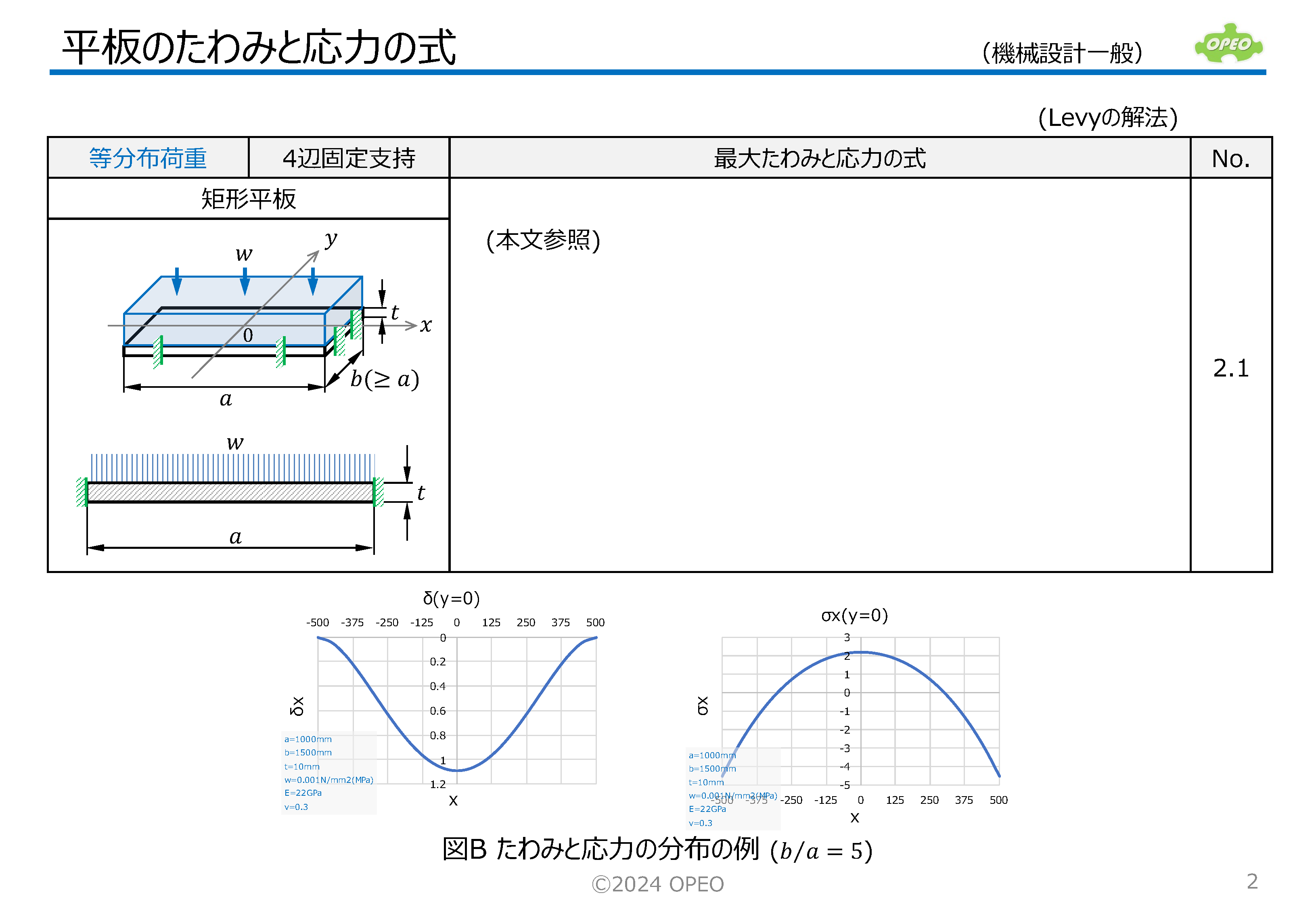
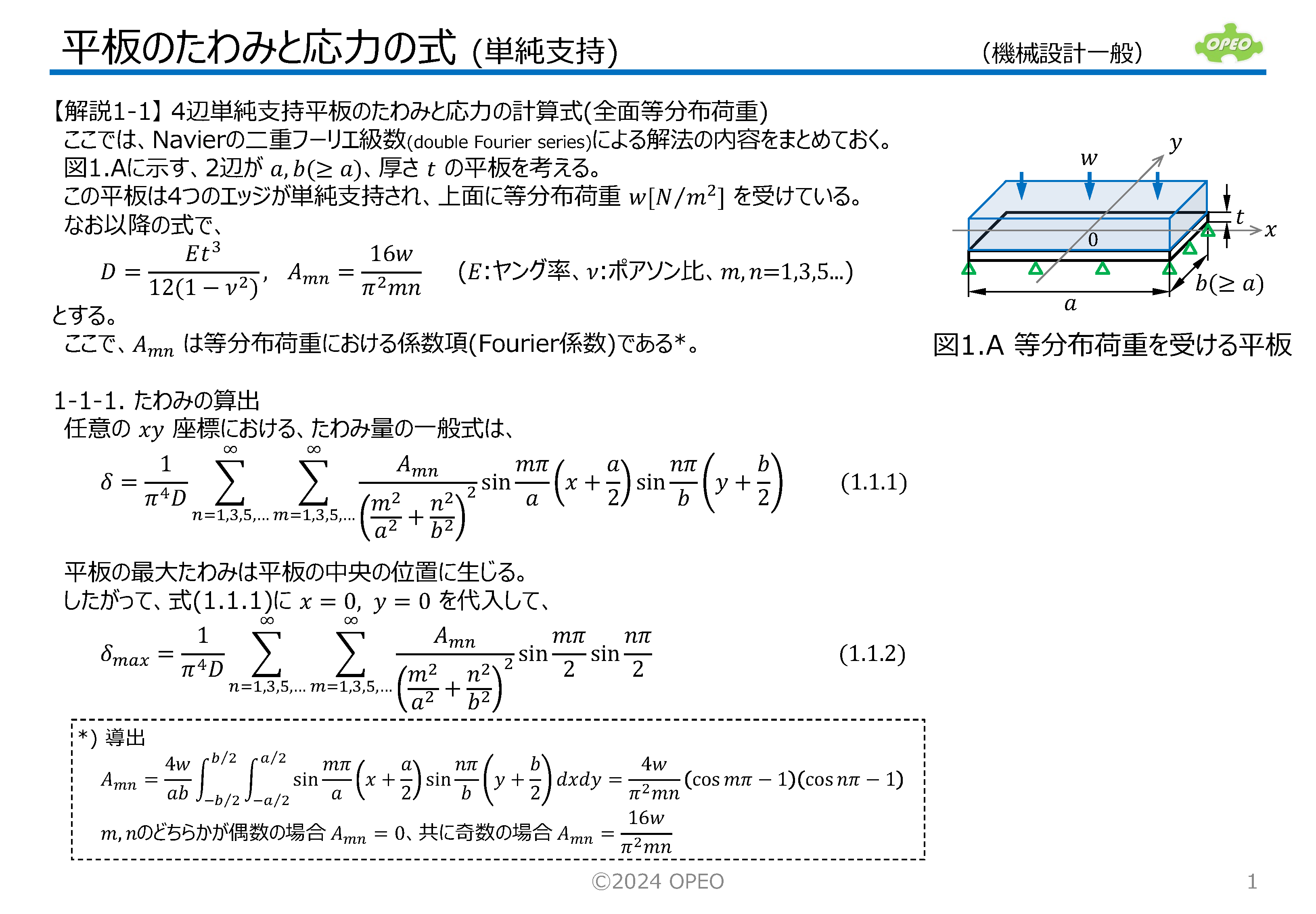
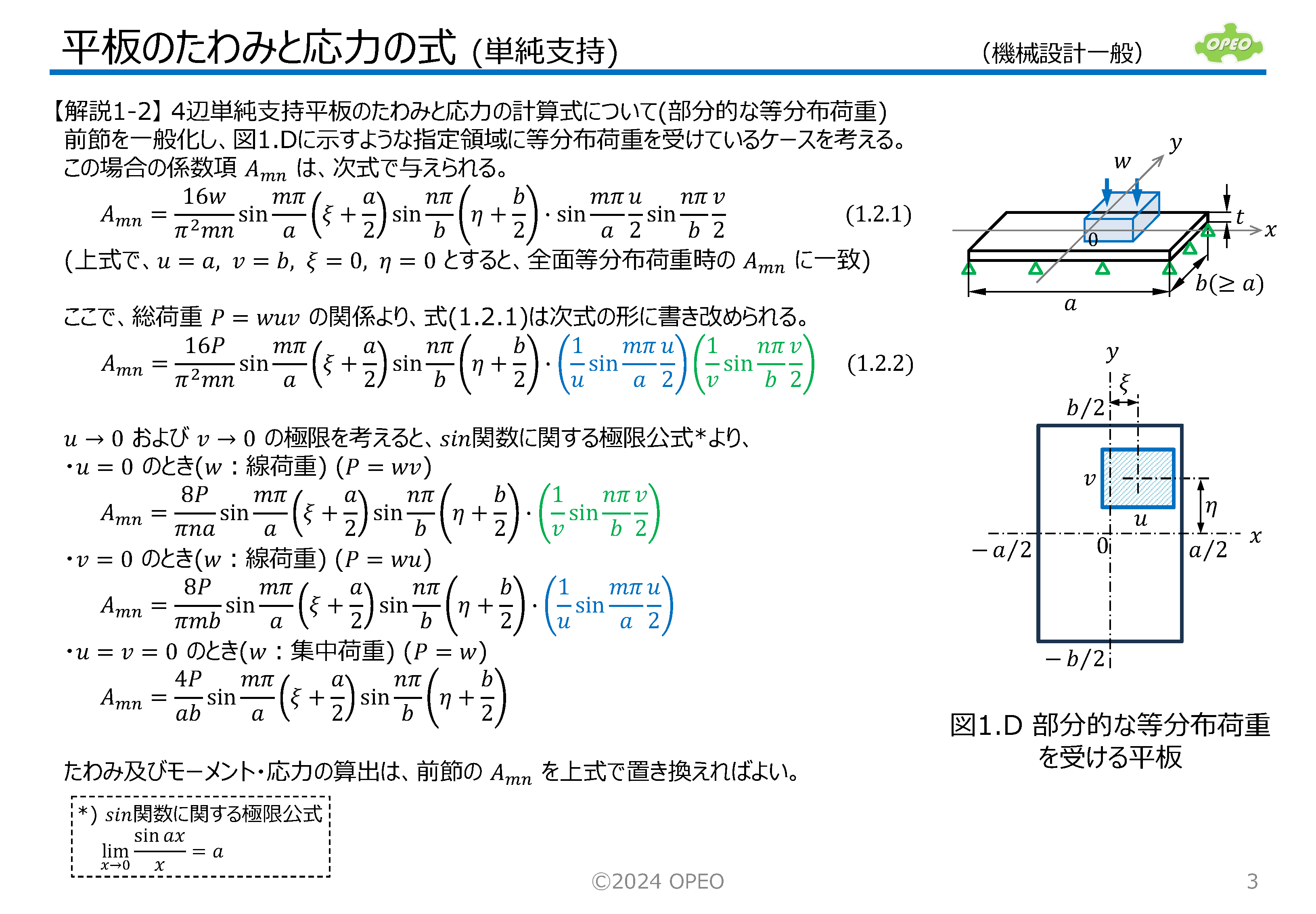
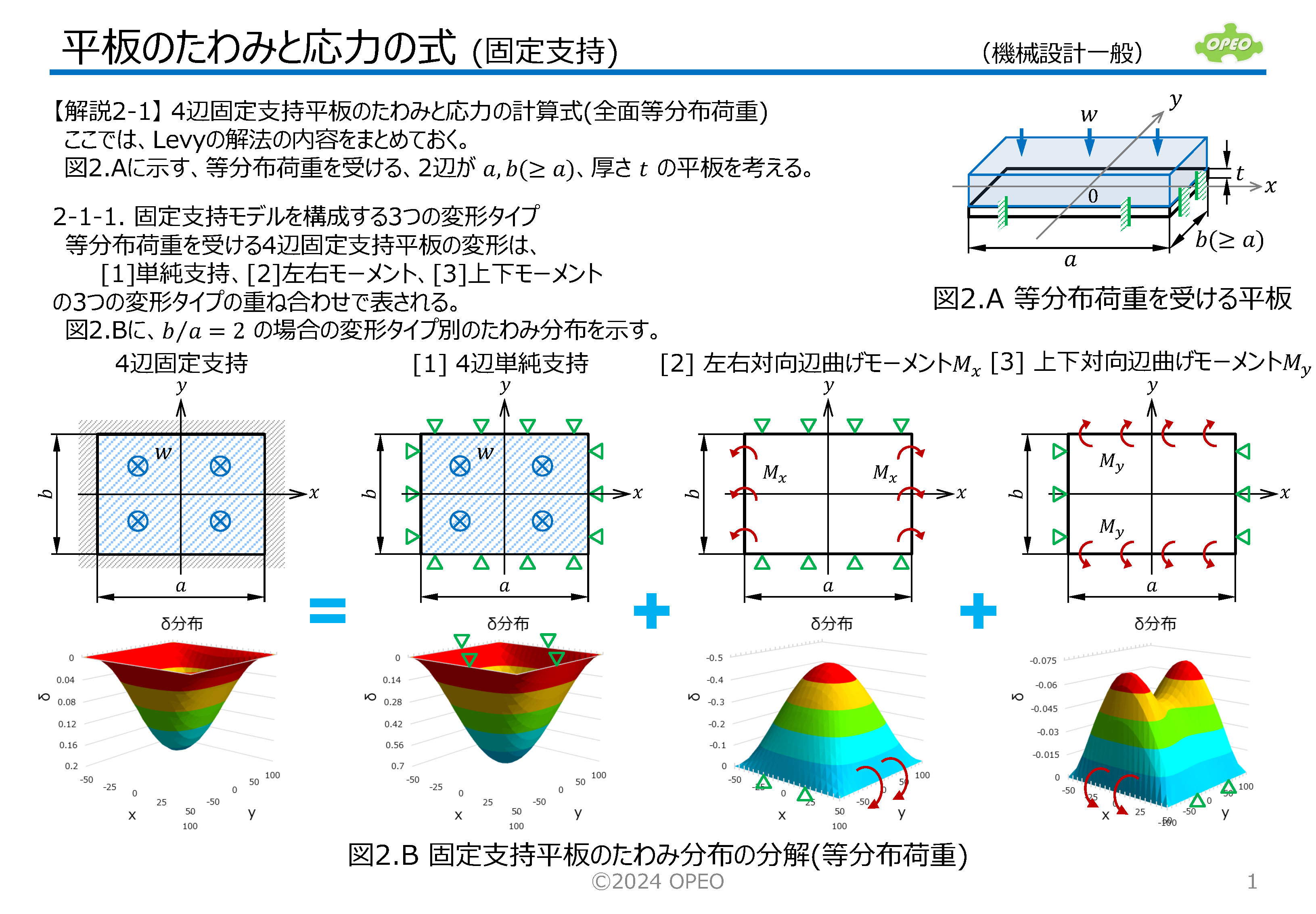
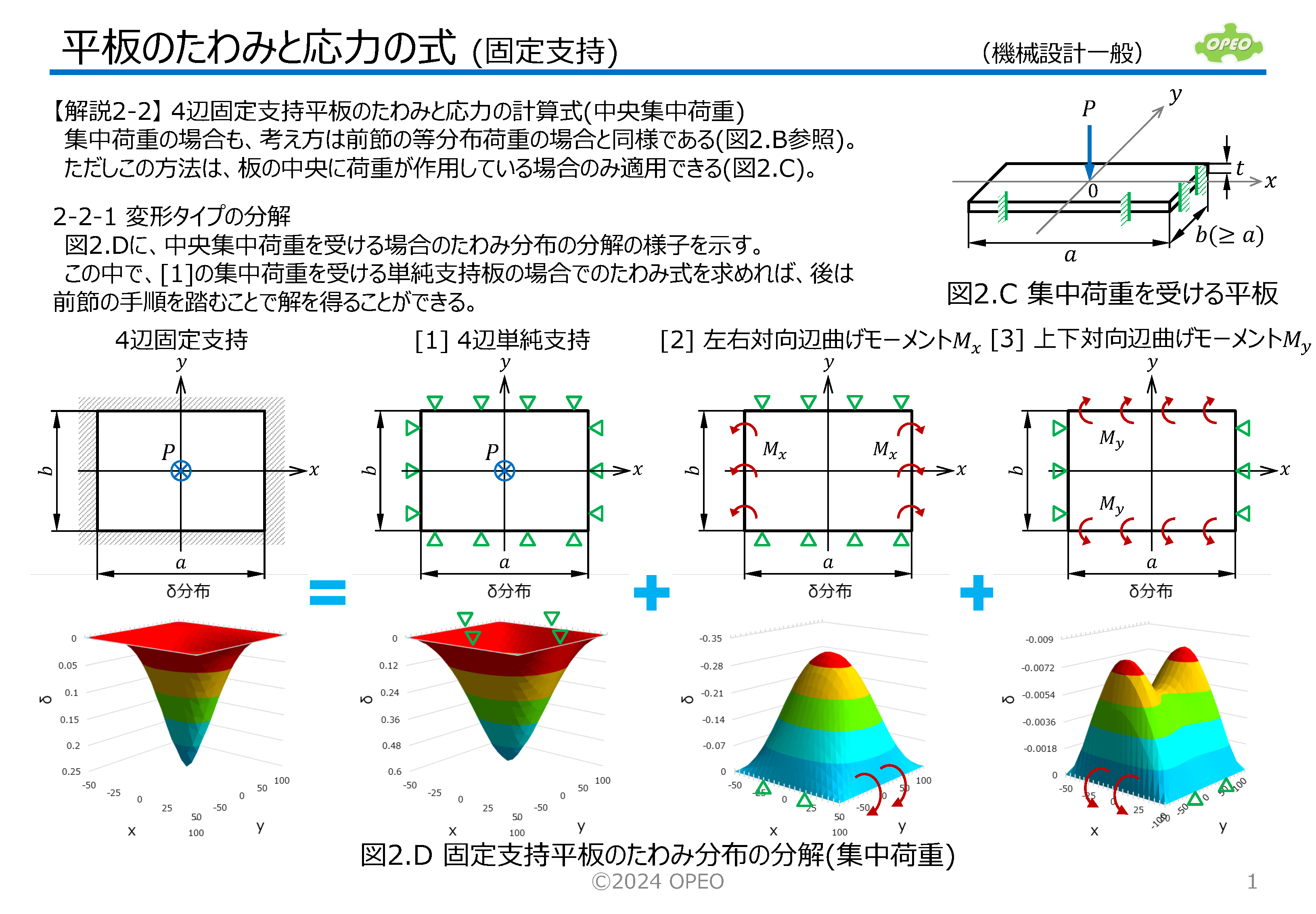
4辺が単純支持または固定支持され上面に等分布荷重を受ける、矩形平板のたわみと応力を求める式をまとめたものです。 一般には、ポアソン比(ν)を固定して最大たわみと最大応力を求める計算式が多いのですが、ここでは任意のポアソン比に対して任意のxy位置のたわみと応力を求める、より汎用的な計算式を紹介しています。 本稿の計算手法は、二重フーリエ級数を用いたNavierの解法と、単級数を用いたLevyの解法と呼ばれるものです。 b>aの場合の、モーメントMyの分布が鞍馬形になることに注目して下さい。 なお、式中のモーメントの定義で、Mxはx方向の応力を発生させるモーメントであり、xの位置におけるy軸回りのモーメントを意味します(Myについても同様)。 本記事に記載の計算方法を用いたExcel計算シートを公開しています。 |
等分布荷重のイメージ図 |
＜参考文献＞
・S.Timoshenko (1959), “Theory of Plates and Shells”, McGraw-Hill, pp.105-124
・堀井,本 (1968), “解析法による版の曲げモーメント数値表“, 港湾技研資料, pp.35-46
<参考URL>
・森設計企画 平板の計算の基礎
・efunda:Simply Supported Rectangular Plates (検算用)
・efunda:Clamped Rectangular Plates (検算用)
・角板変形(全周支持、等分布荷重) (検算用)
・角板変形(全周固定、等分布荷重) (検算用)
・角板変形(全周支持、中心集中荷重) (検算用)
・角板変形(全周固定、中心集中荷重) (検算用)
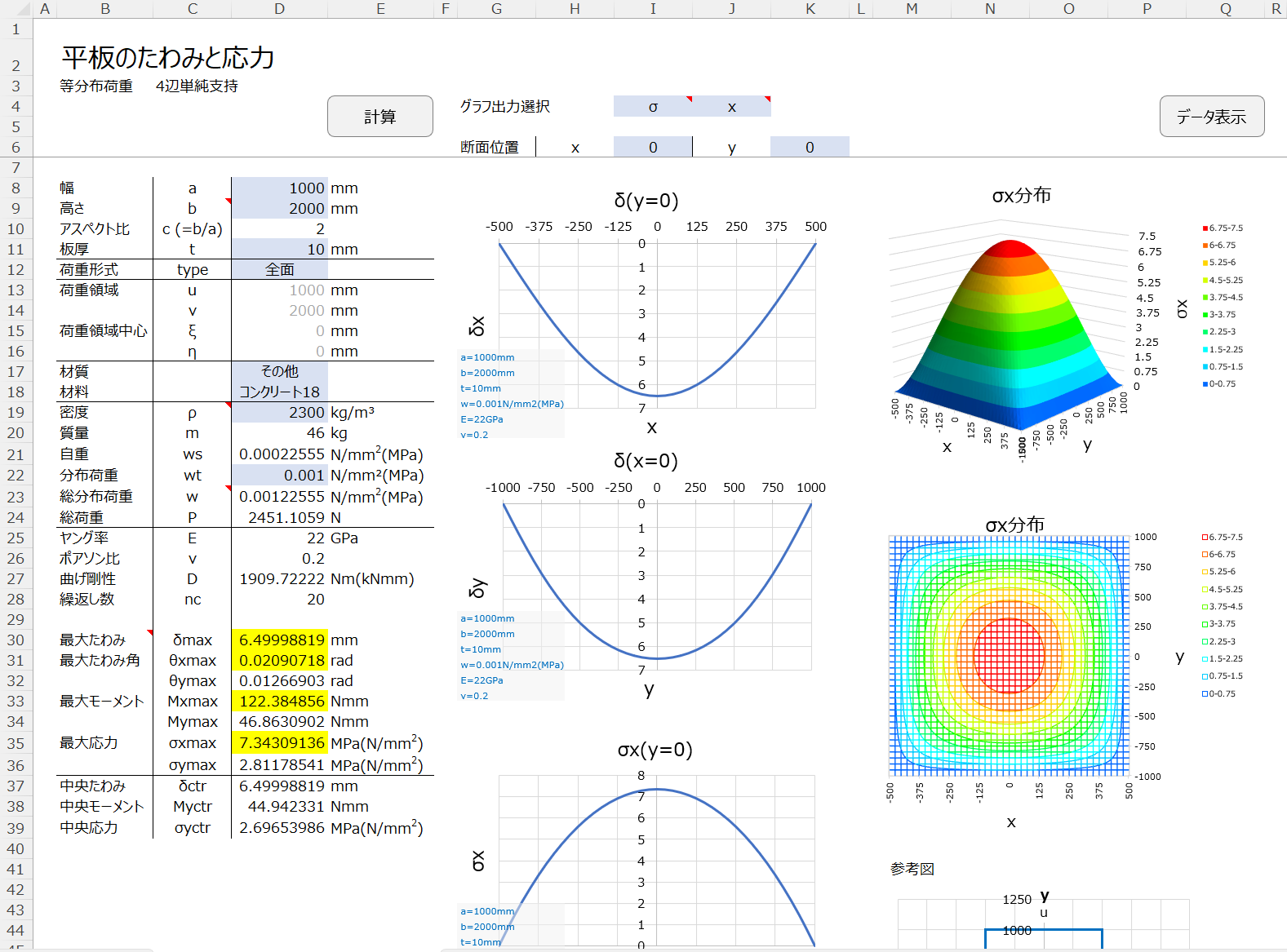
平板のたわみ計算Excel
外縁を単純支持または固定支持された矩形平板に等分布/集中荷重が作用した場合の、たわみと応力を計算するExcelシートです。
x,y軸が板の中心を通る場合での計算を行っています。
青網掛けのセルに数値を入力後に計算ボタンを押すことで、結果が更新されます。
材質と材料をプルダウンメニューから選択すると、対応した物性値をセットします(revF以降)。
（材料データシートはカスタマイズ可能)
revE以降では、単純支持の場合は指定範囲の分布/集中荷重、固定支持の場合は中央集中荷重でのたわみと応力計算を試験的に実装しています。
・単純支持の場合：D11セルを「指定領域」に切り替えて、D12/13セルに領域サイズを入力
・固定支持の場合：D11セルを「集中荷重」に切替え
revF2以降では、グラフ用の計算データ列の表示・非表示を切り替えるボタンを追加しています。
revG以降では、プログレスバー表示のON/OFFスイッチを付けています。
マクロのソースにはロックはかけていませんので、興味のある方は中身を確認してみて下さい。
2024.10.4 更新 (revG1→revG2)
