カム
7,863
|
カムは、直線運動と回転運動の相互変換や方向変換など、メカニズム設計には重要な機械要素です。 |
|
§ 目次
<カム曲線>
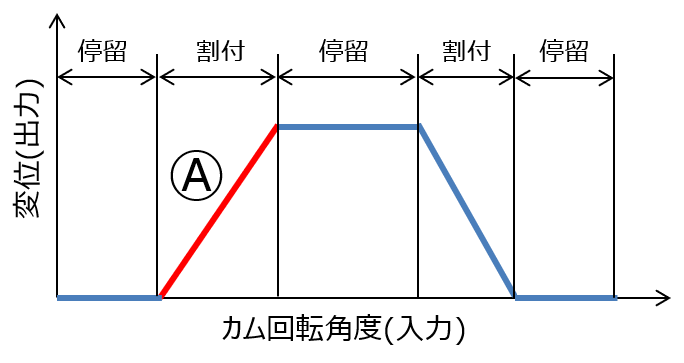 |
カム曲線の考え方 |
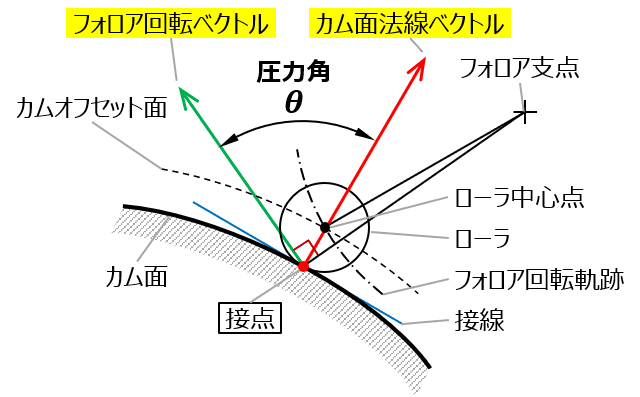 |
カムの圧力角 |
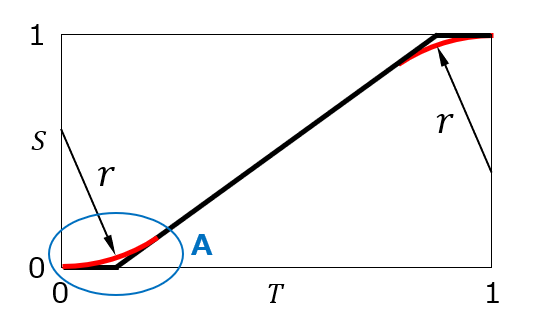 |
正接円弧カム曲線 |
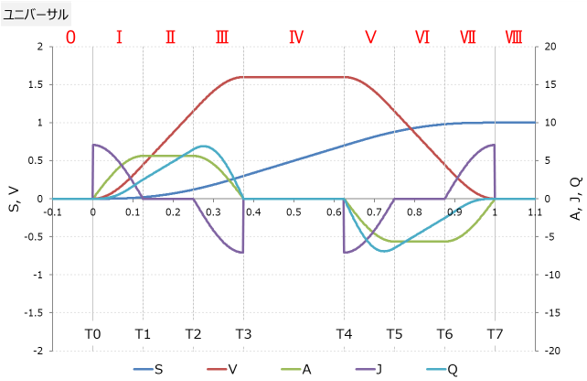 |
ユニバーサルカム曲線 |
機械設計の技術支援とコンサルティング
7,863
|
カムは、直線運動と回転運動の相互変換や方向変換など、メカニズム設計には重要な機械要素です。 |
|
§ 目次
 |
カム曲線の考え方 |
 |
カムの圧力角 |
 |
正接円弧カム曲線 |
 |
ユニバーサルカム曲線 |