FAQ
よくある質問を掲載
5,524
§ 目次
【幾何公差関係】
(★印はミニ講座ー幾何公差編の中で紹介しているものです)
| Q | 幾何公差を使うとコストが上がる、と言われたのですが。 | |
| A | 幾何公差は、一つには部品の形状定義の曖昧さを無くす目的で使いますが、多用し過ぎるとそれだけ加工や検査コストが上がる可能性はあります。 そのため、設計上重要な箇所に対して用いるようにした方がよいでしょう。★ また、最大実体公差方式(MMR)を適用すると検査コストそのものを減らすことも可能です。★ |
|
| Q | 幾何公差を入れても加工メーカー側がそれを理解できないのではないですか? | |
| A | 以前はそのような事例もありましたが、最近は幾何公差図面の出図率が上がりそれに応じて多くのメーカーが理解できるようになってきています。 資材、調達部門の協力による非対応メーカーさんへの啓もう活動も効果があります。 (なお当方ではそのようなメーカー指導も承ります) |
|
| Q | 幾何公差で指示した図面の検図をしてもらいましたが、上司から「意味が分からないから元の書き方に戻してくれ」と言われました。 | |
| A | 上司も忙しくて、今更幾何公差の勉強をして下さいとは言いにくいかもしれません。 特に位置度や輪郭度などは、記号を見てもピンと来ないかもしれません。 苦肉の策ではありますが、まずは平行度や直角度など誰が見ても意味がわかるような記号を盛り込んでみる方法はあるかと思います。それらの記号に円筒公差域Φを指示する使い方だけでも、形体定義はかなり明確になってきます。 |
|
| Q | TED(理論的に正確な寸法、理論寸法)を使ったらメーカーさんから意味を聞かれたので「誤差のない寸法です」と答えたら「そんな加工はできません」と言われました。 | |
| A | TEDは、基本的に単独で使われるものではなく(←例外はあります★)、位置度や輪郭度など一部の幾何公差記号と組み合わせて使われます。 TED自体は確かに誤差を含まない値ですが、その誤差(ばらつき)範囲を例えば位置度の公差域により指定していると考えます。これは結局、従来の寸法表記における図示サイズとサイズ公差の関係と同じです。 |
|
| Q | 3次元測定機がないと幾何公差の測定は難しいのですか? | |
| A | 3次元測定機(CMM)を使えば、殆どの幾何公差の測定は可能ですが、従来からある汎用の測定機器でも検査は可能です。★ むしろ、このような汎用機器類で測定した方が効率が良いケースは多々あります。 ただ、輪郭度で指示した形状(デザイン意匠面など)の測定は、CMMやデジタイザ(非接触CMM)を利用した方がいいでしょう。 |
|
| Q | 幾何公差の指定の仕方と測定方法はどれだけ連携する必要があるでしょうか? 機能上必要と考えれば、測定方法はいったん脇に置いて幾何公差を設定して良いものなのでしょうか? |
|
| A | どのように測定するかは常に意識する必要があります。 測れないものは作れないからです。 |
|
| Q | 幾何公差を入れると図面がにぎやかになります。もっとすっきりさせた書き方はできませんか? | |
| A | 幾何公差指示図面は、データムや幾何公差記入枠が大量に書き込まれるケースもあるため、一見して図面が複雑怪奇なものに捉えられがちですが、以下の点に注意するといいです。 ・設計上重要な箇所だけに絞って幾何公差指示を入れる。 ・適切に投影図(View)を追加して記述を分散させる(一つの投影図に何でもかんでも押し込むのは製図作法としてもスマートではありません)。 ・場合によっては普通幾何公差の導入も検討する。★ |
|
| Q | 中心軸が平行な2つの穴への共通データム指示と、形体グループのデータム指示の使い分けについて | |
| A |
違いは、共通データムの場合、2つの穴径が異なる(形体が異なる)
加えて、共通データムは2つの穴(形体)しか対象にしませんが、
従って両者の使い分けは、
・形体が異なるかどうか
・対象が3つ以上か否か
で選択すればよいと考えます。
|
|
| Q |
幾何公差には、例えば+0.2/-0.1のような不均等公差の指示方法はないのですか?
|
|
| A |
ASMEやISOでは既に不均等公差の指示方法が規定されています。★
例えばISOでは、0.2 UZ+0.05 のように理論形体(TEF)に対して0.05だけ外側にオフセットした仮想面を基準として0.2の幅の公差域を定義する、という記述法が定められています。 JISもいずれISOに合わせて取り入れてくるでしょう。 |
|
| Q |
振れと真円度/円筒度の違いは?
|
|
| A |
振れは、軸の中心線を回転軸として回転させながら、ダイヤルゲージなどを用いて表面の凹凸を評価します。
一方、真円度や円筒度は、円の中心の位置には関係なく表面の凹凸が真円に対してどれだけずれているかを評価するもので、一般的には真円度測定機を用いて測定を行ないます。 なお、圧入軸のような回転させない円筒部品に対して振れを指示するのは、過剰スペックともなり得るため注意が必要です。 |
|
| Q |
平行度と位置度の違いは?
|
|
| A |
平行な2平面間に対して平行度と位置度を指示した場合で、通常の加工精度であれば似たようなものができあがるかもしれません。
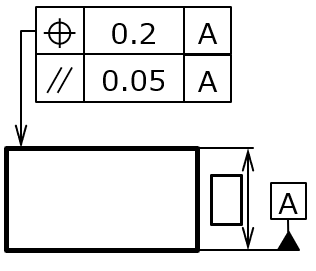
2つの指示方法の大きな違いは、平行度はあくまでもデータム(基準面)に対する平行性がとれていればよい、というのに対し、位置度はデータムからの距離のばらつきも含めて平行性を確保しなさい、という点です。 位置度公差には平行度も含まれるため、必要以上に距離の精度が高いということも起こり得ます。
2面間の距離は2点間測定レベルの精度でよいのであれば、平行度指示だけで十分です。
なお、データムからの距離のばらつきは緩めでも良いが、平行性は厳しくしたい、という場合は、位置度と平行度を組み合せた幾何公差指示方法を選択する、という方法もあります(右図参照)。
|
 |
【公差分析関係】
| Q | 平行度指定面の傾きによる高さ変化の計算を、公差域の幅の中心位置から振っている理由(公差計算と幾何公差2) |
| A |
平行度指定面の傾きの計算が、穴ー軸のクリアランスによるガタの計算と解法手順が同様になるように考えているためです。 |
【Excelツール関係】
| Q | 圧入計算シートで周方向応力が赤色に表示される理由 |
| A |
周方向応力が穴側材料の引張強さを安全率で割った値より大きい場合に、赤色表示されるようにしています。 |
| Q | 圧入計算シートで結果表示セルに「#NAME?」と表示される |
| A | マクロの実行がExcelのセキュリティ設定により中断されている可能性があります。 その場合はマクロの有効化(コンテンツの有効化)を行なって下さい。 |
| Q | ユニバーサルカム曲線シートで切削送りのカーブが描けない【解決済み】 |
| A | アルゴリズムを見直しました。 revC(’20 5/20リリース)以降で、正しく切削送りカーブが生成できるようになりました。 |
【機械設計関係】
| Q | 歯車の標準圧力角が20°の理由 |
| A |
ざっとネットの記事を調べた結果ですが、 ・昔は圧力角は14.5°とか17.5°というのがあった。 ということのようです。 |
| Q | |
| A |
