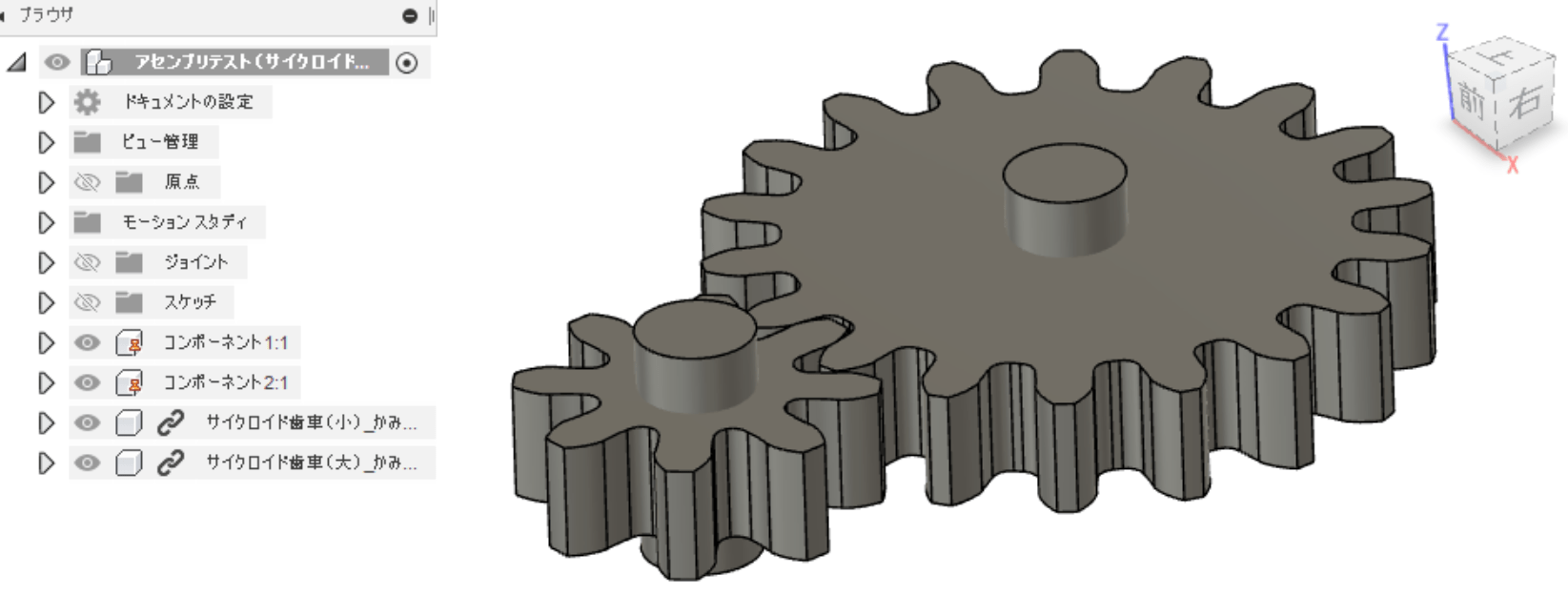
歯車
10,624
|
歯車設計の技術資料としては、小原歯車工業㈱の歯車技術資料が秀逸です。 特に、歯形曲線の交点座標や歯形係数の導出手順は、解説した資料があまりないため、参考になると思います。 |
|
<参考URL>
歯車の設計とモデリングツール-involutegearsoft
掲載記事に関連した動画をYouTubeで公開していますので参考にして下さい。
§ 目次
<歯形曲線>
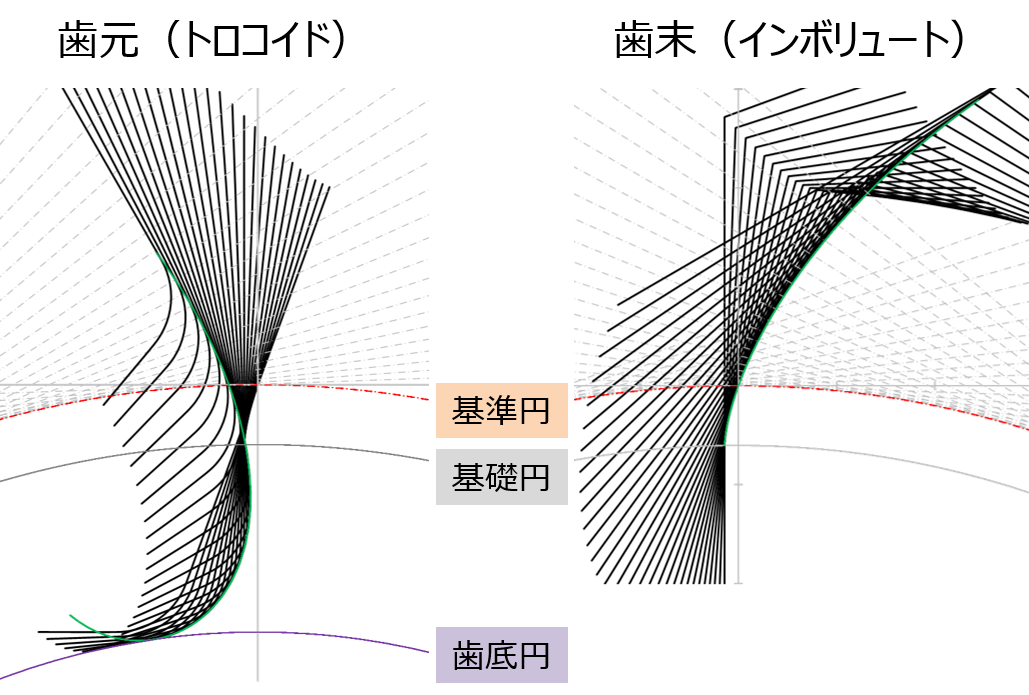 |
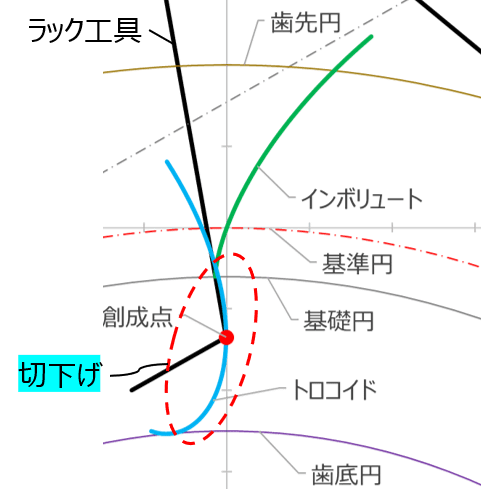
歯形創成曲線 |
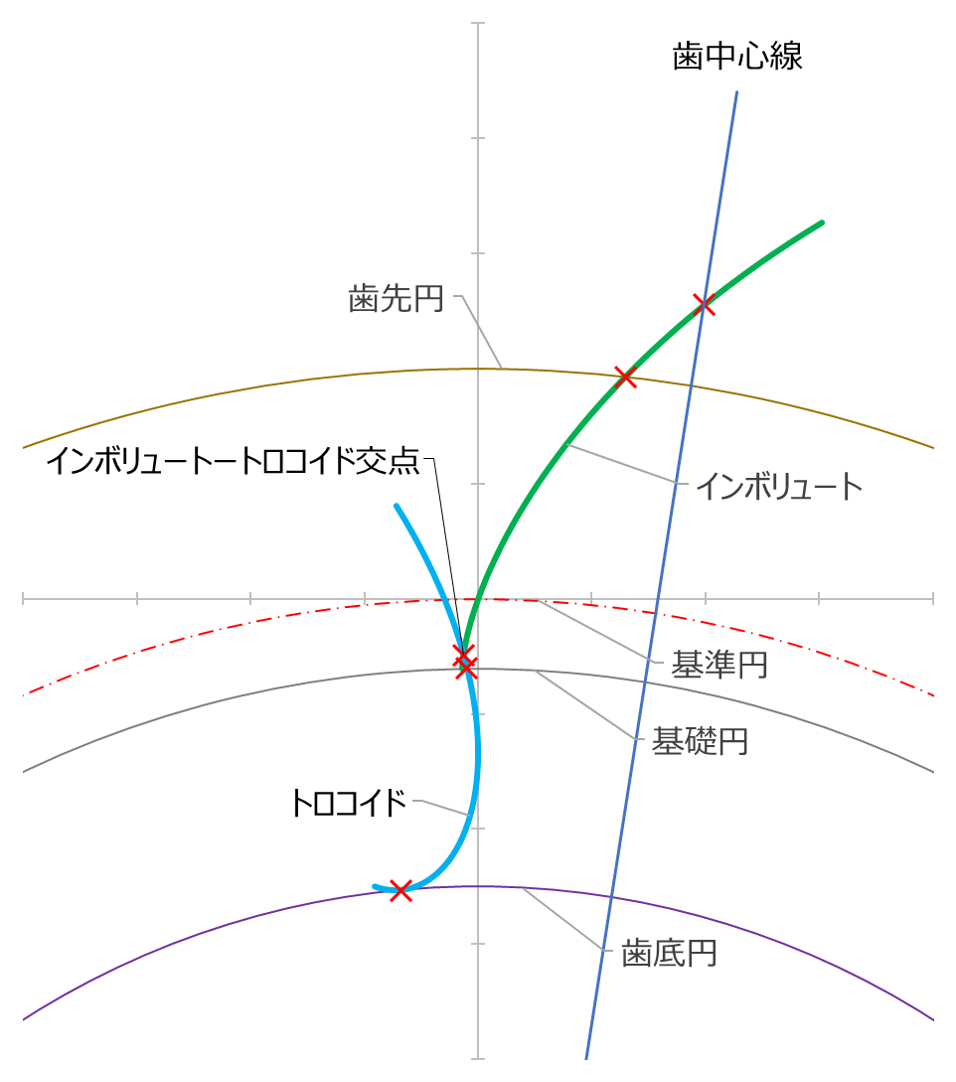 |
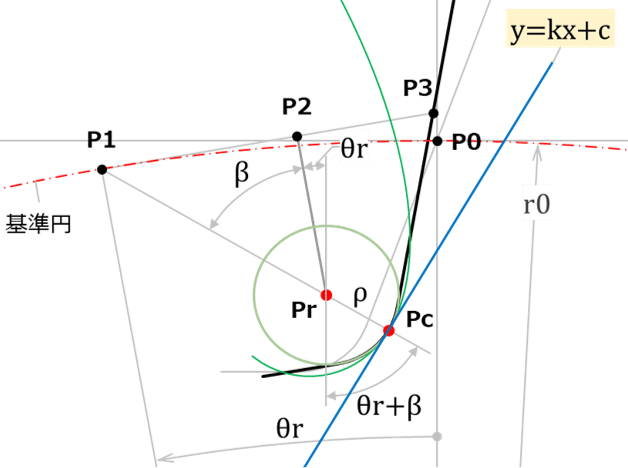
歯形曲線上の点の座標 |
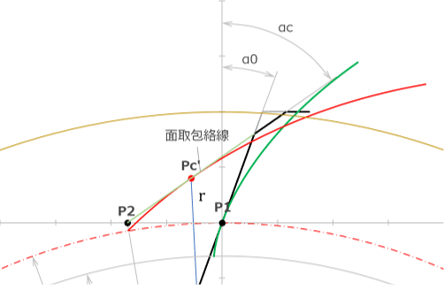 |
セミトッピング形状の創成 |
 |
歯形曲線の接線 |
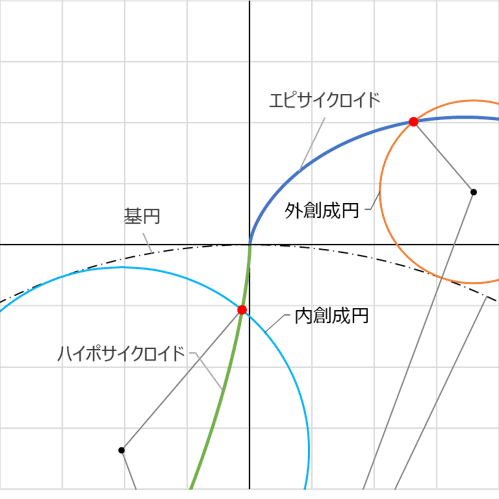 |
サイクロイド歯形曲線 |
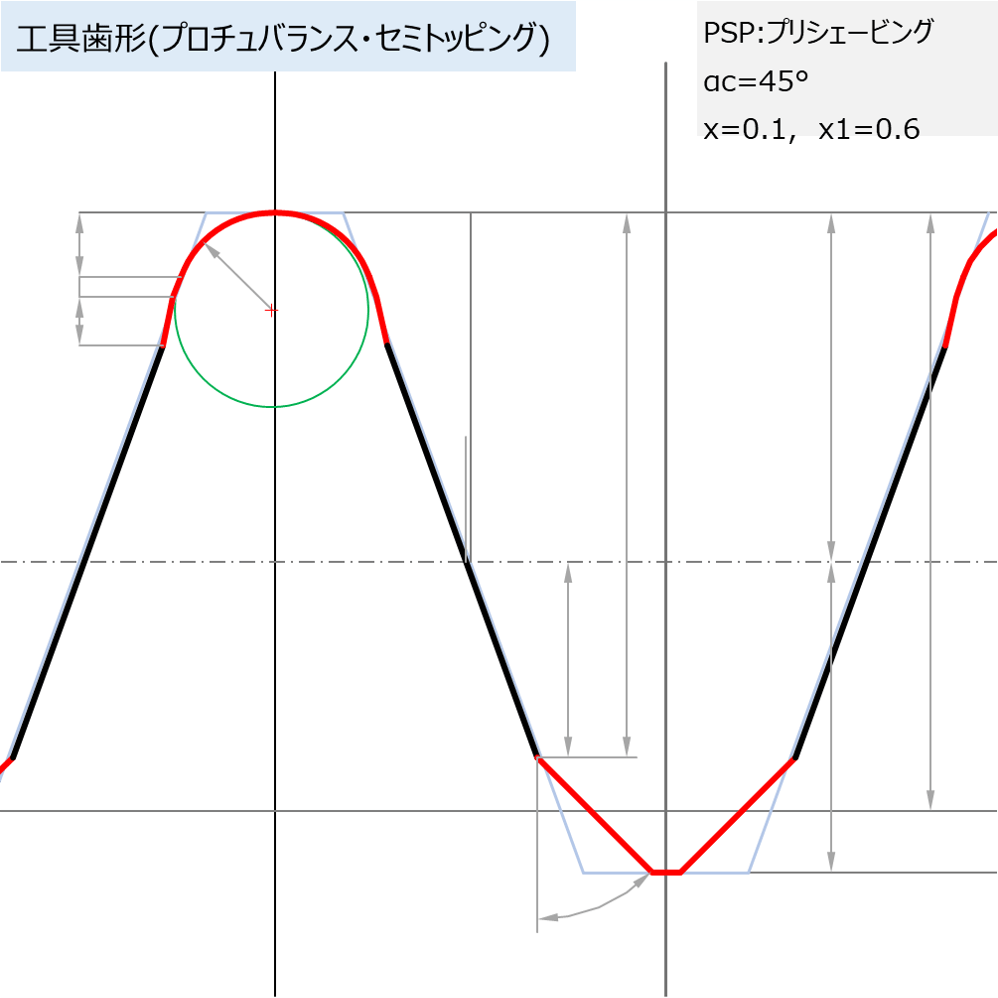 |
歯切工具歯形 |
<歯形係数>
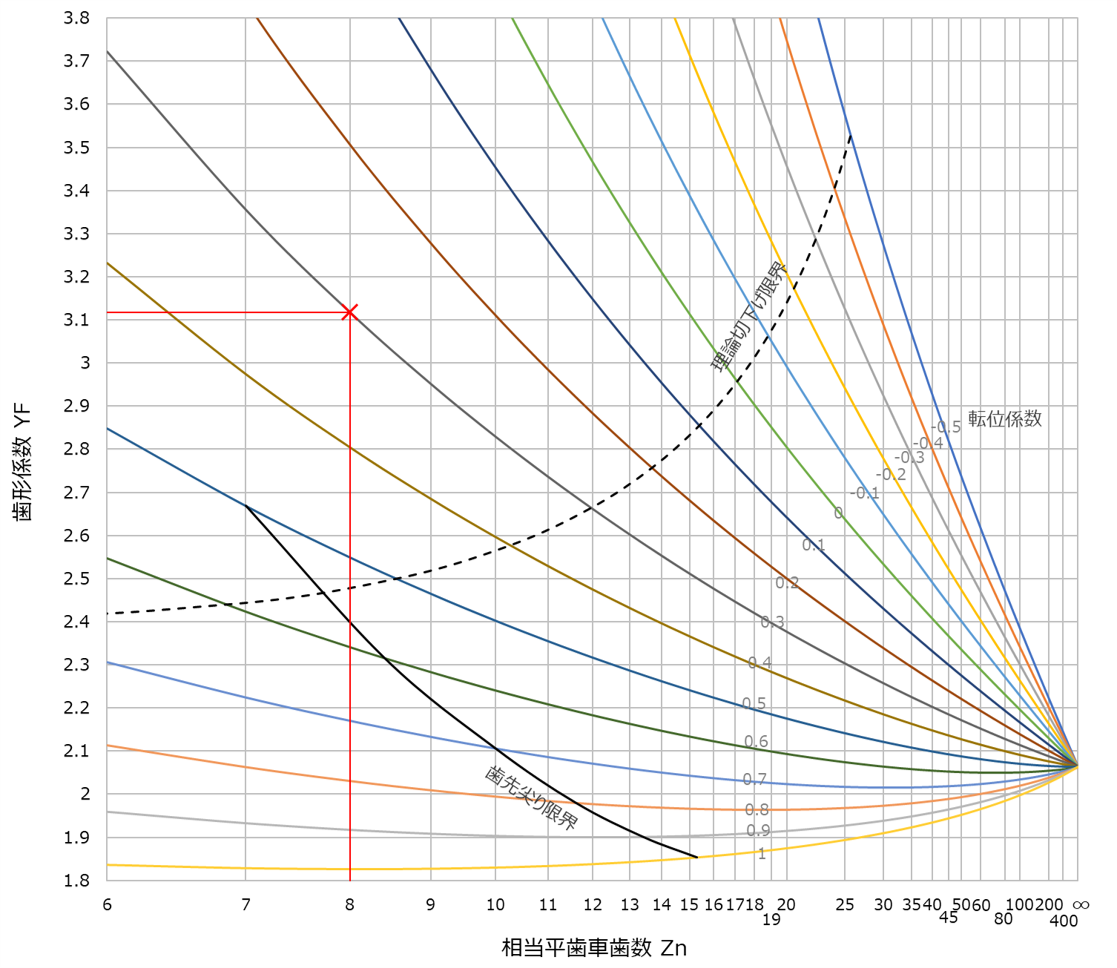 |
歯形係数 |
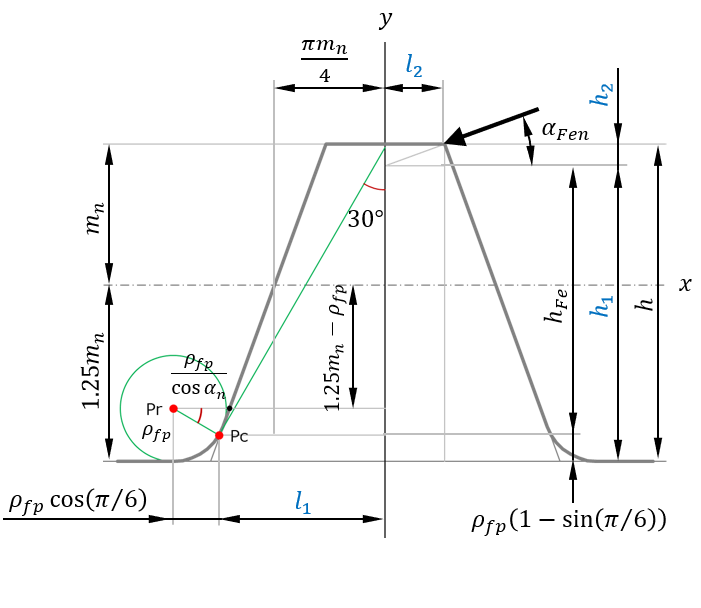 |
ラックの歯形係数 |
<その他>
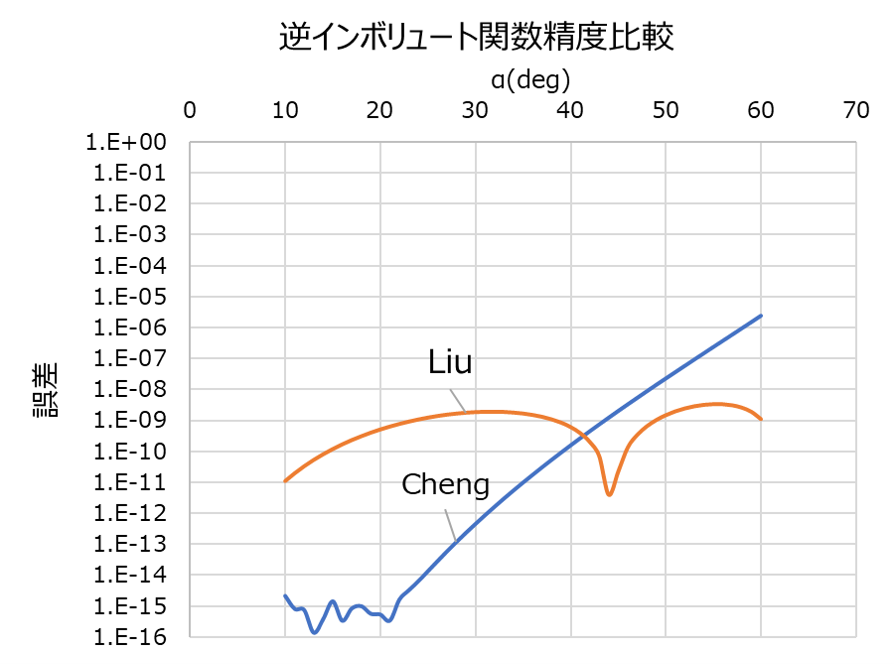 |
逆インボリュート関数 |
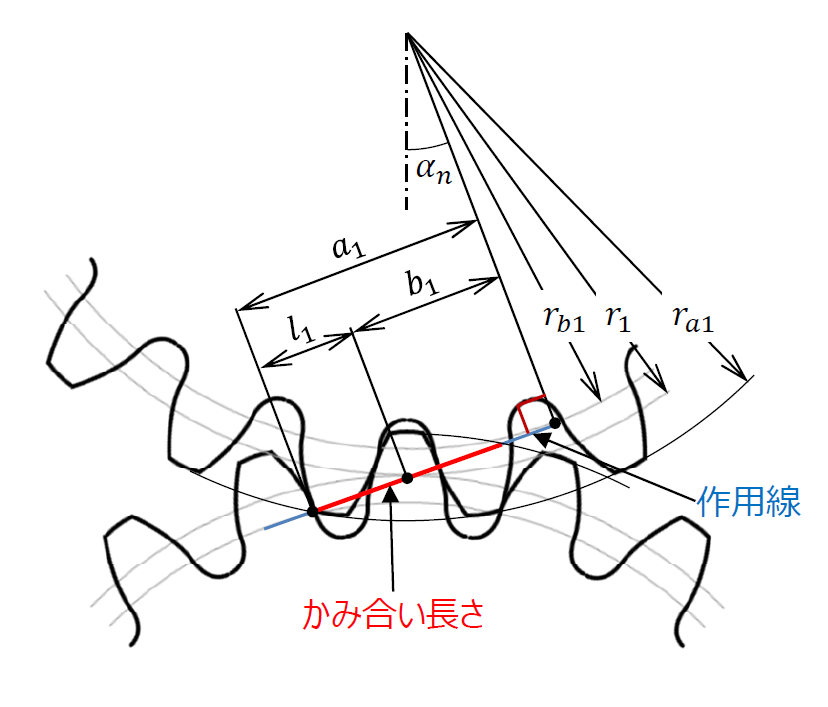
かみ合い率 |
|
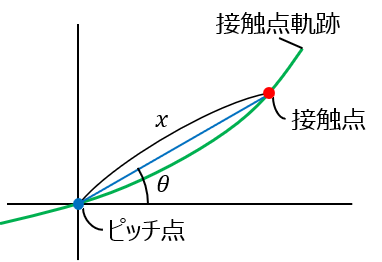 |
すべり率 |
|
切下げ限界歯数 |
<参考動画>