逆インボリュート関数

9,594

 

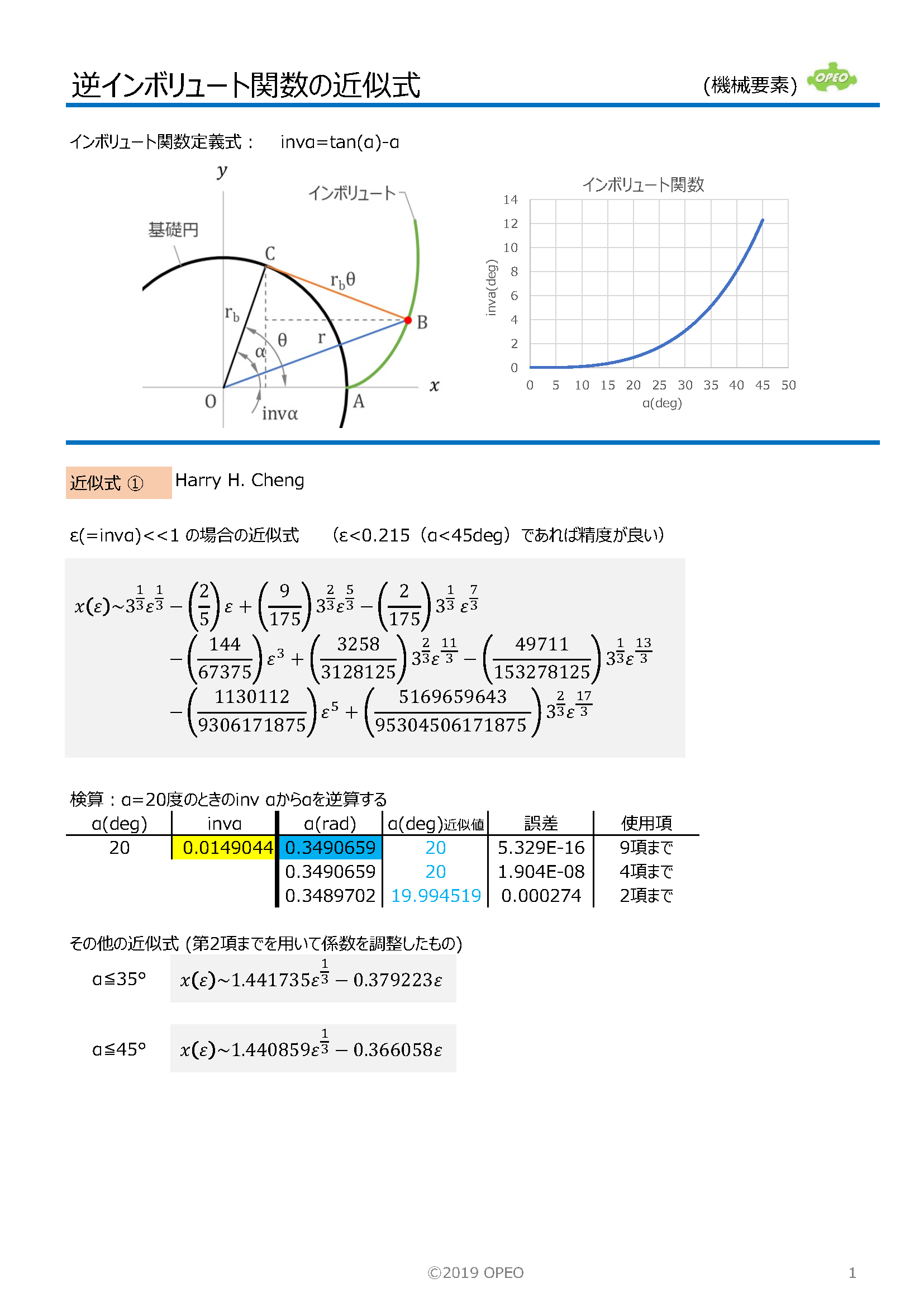
　インボリュート関数（invα）は、右上図の角度αを用いて、次式で求められます。

invα = tan(α) – α

　逆インボリュート関数は、invα の値から α を求めるものですが、これにはいわゆる解析解がありません。

　一般的には、関数表の利用や、ニュートン・ラフソン法や二分法による近似計算方法が知られていますが、反復計算を伴わない、多項式による近似式も公開されています。

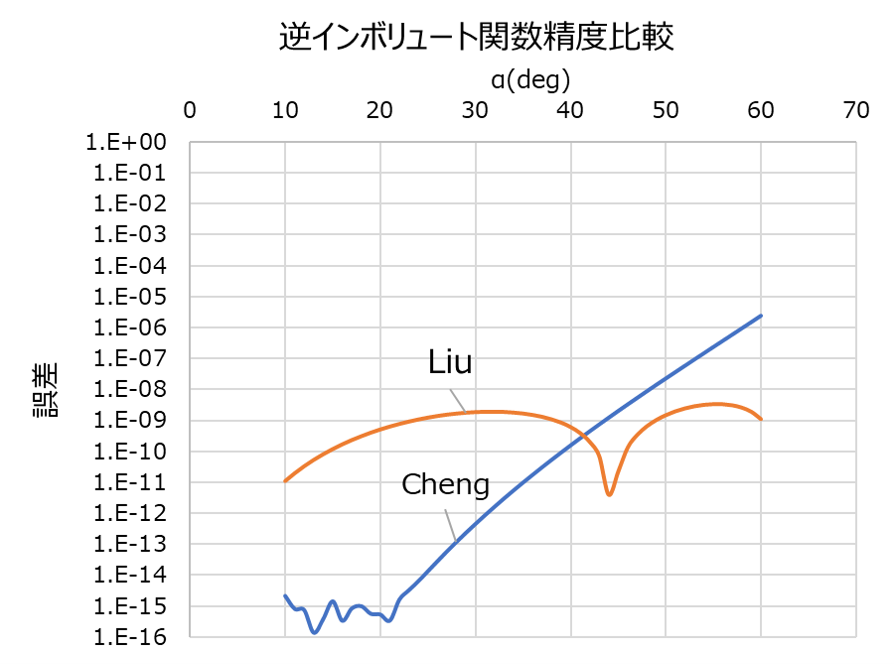
　多項式によるものは、方式により誤差が異なりますが、実用的にはどれも十分利用可能です(右下図参照)。
　(本サイトの計算資料では、基本的にVBAコードによるニュートン・ラフソン法を使っていますが、VBAを用いない場合は、ここで紹介する多項式近似を利用するとよいでしょう)

　なお逆インボリュート関数の値は、転位歯車のかみ合い圧力角の計算(最終的には転位歯車対の中心距離計算に使用)や正面かみ合い率、歯形係数の計算にも用いられます。

　ユーザー定義関数(UDF)として使用できる、Excelのマクロファイルも添付します。

 

<参考文献>

・Harry H. Cheng (1996), “Derivation of the Explicit Solution of the Inverse Involute Function and Its Applications in Gear Tooth Geometry Calculations “, Journal of Applied Mechanisms & Robotics, Vol. 3, No. 2

・Irving Laskin (2005), “Calculated Bending Load Capacity of Powder Metallurgy (P/M) External Spur Gears”, AGMA 930-A05

・Irving Laskin (1993), “Solving for the Inverse “Sevolute Function””

・Q.Liu (2017), “The Solution of Inverse Involute Function on Non-iterative Method and High Precision”, Journal of Yangzhou Polytechnic Institute, No. 2017(1)

・A.L. Rosado et al. (2019), “An Analytic Expression for the Inverse Involute”, Mathematical Problems in EngineeringVolume 2019, Article ID 3586012, Hindawi

 

 

逆インボリュート関数 Excelマクロ

　上記で紹介した近似式の、Excelマクロのソースファイル(.bas)です。

　関数名：calc_invinv(n, x)
　引数 n により、計算方法を切り替えます。
　　1：近似式① (Chengの式)
　　2：近似式④ (Liuの式)
　　3：ニュートン・ラフソン法 (最高精度)

　引数 x に、インボリュート関数値をセットすると、逆インボリュート関数値を返します。

　Excelのマクロファイル(.xlsm)にインポートして使用して下さい。

 

2021.8.13 更新 (revA→revB)

DL解除コード：a402

アイコン

逆インボリュート関数

1 ファイル 0.60 KB
ダウンロード