ルンゲ・クッタ法(微分方程式解法)
8,132
|
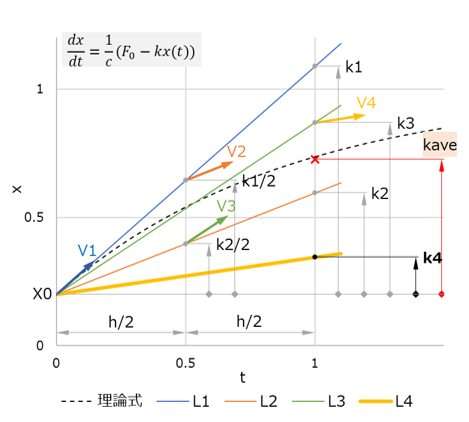
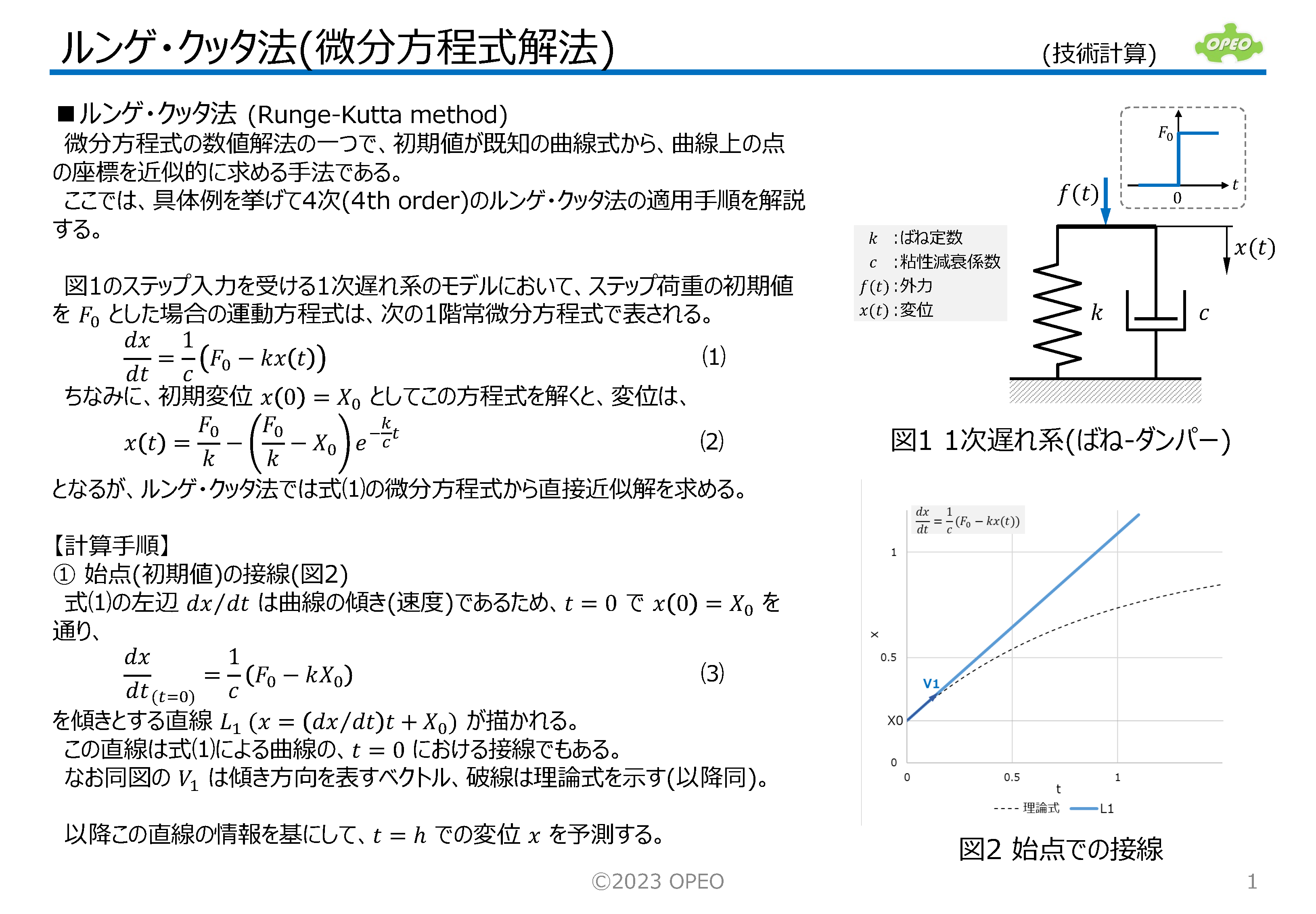
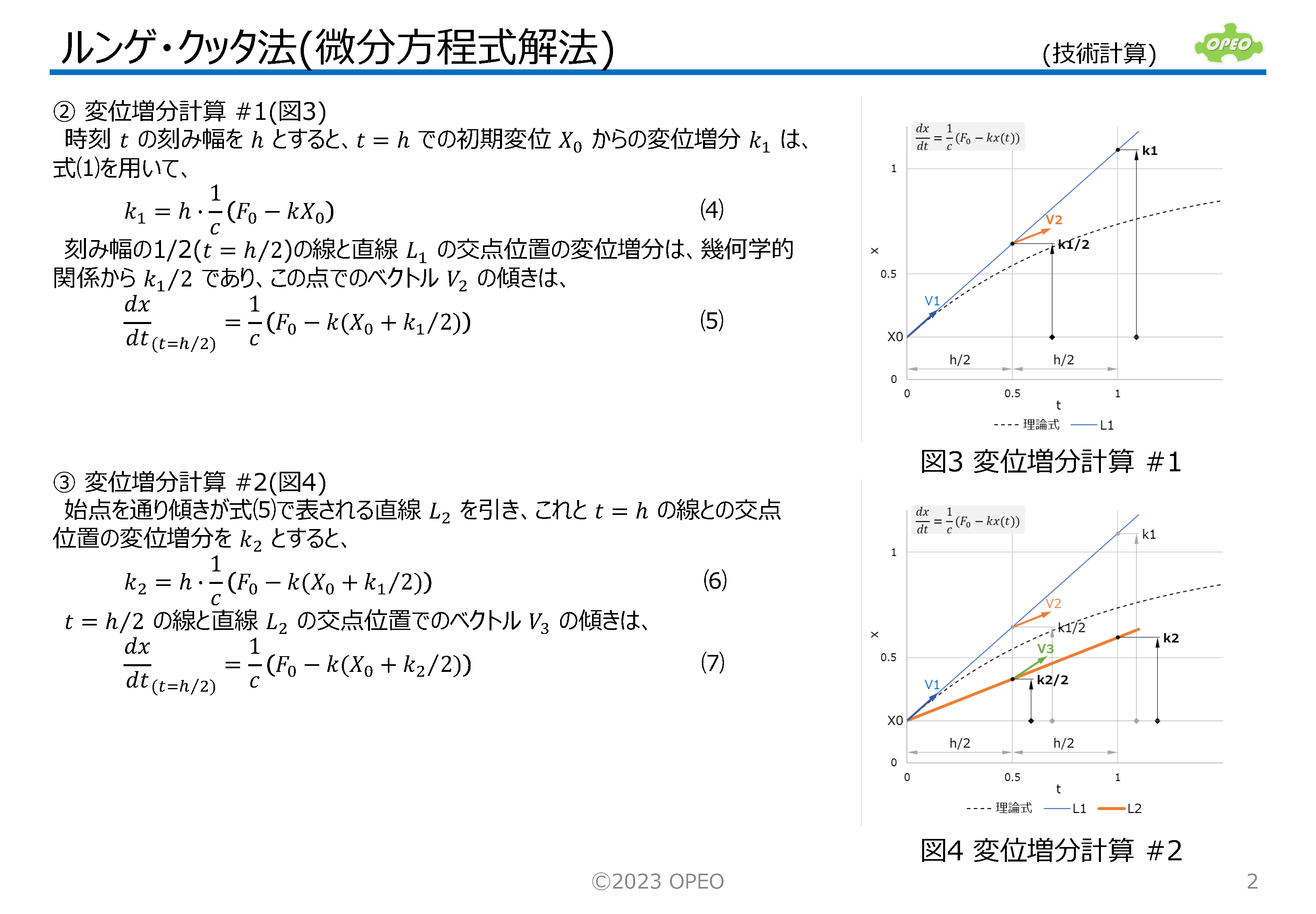
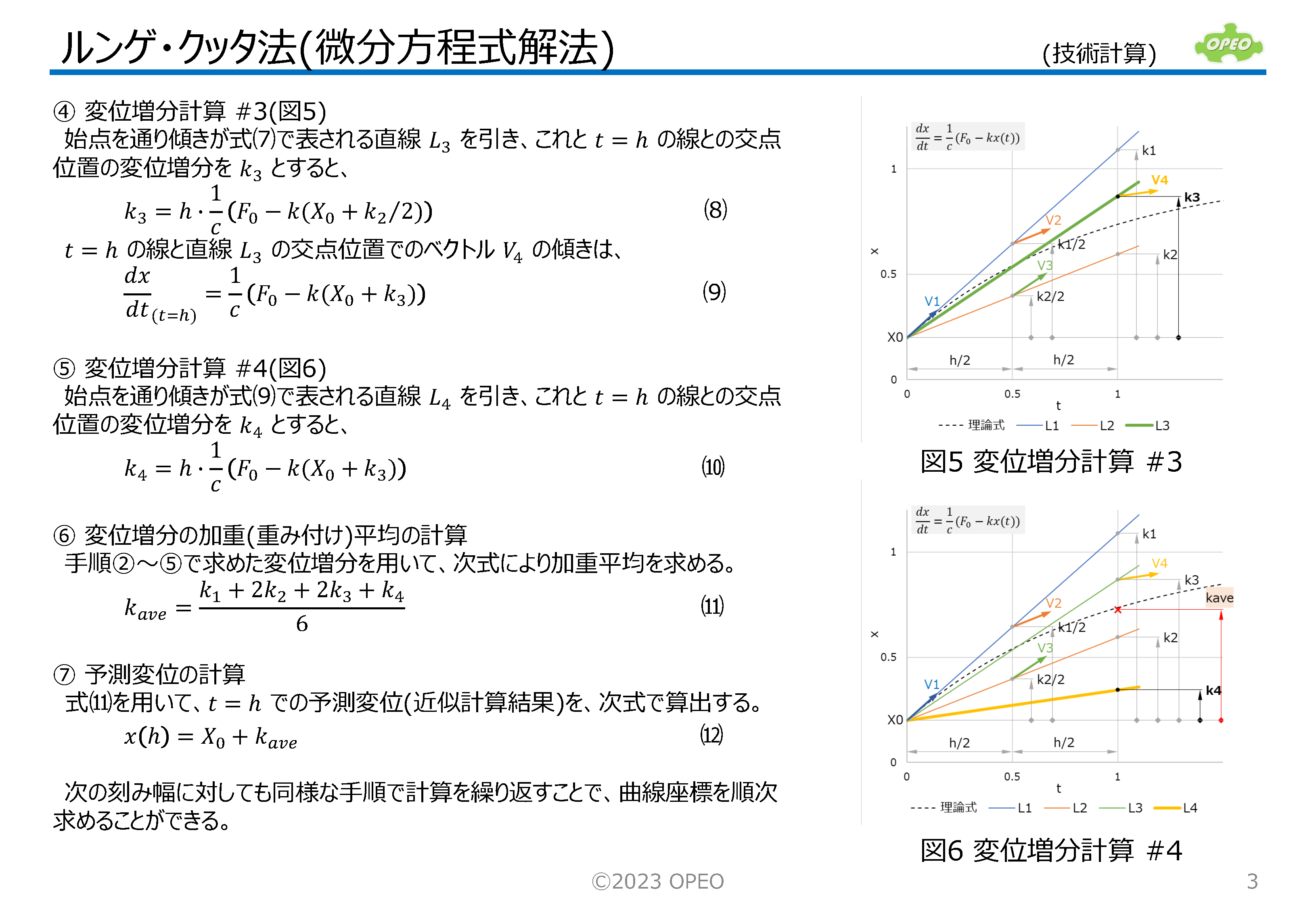
ルンゲ・クッタ法(Runge-Kutta method)は、微分方程式の数値解法の一つで、初期値が既知の曲線の微分方程式から、曲線上の点の座標を近似的に求める手法です。 手順を書き出すとかなりややこしい感じはしますが、プログラム実装は比較的簡単なものになります。 この記事では、制御工学の過渡応答モデルの微分方程式を題材として、この手法の特徴である増分計算の考え方がわかるよう、ステップを追って手順を解説しています。 適用例には、2次遅れ系のPID制御の記述などがあります。 ちなみに、ここで紹介する方法は一般には古典的(classical)ルンゲ・クッタ法などと呼ばれますが、決して骨董品的な手法という意味ではありません。 |
 |
<参考URL>
・数値計算を使って常微分方程式を解く~ルンゲクッタ法の解説~
・微分方程式の数値解法 (2)
・計算数理A演習第7回
・計算物理学2第11回:微分方程式の解法
・Runge-Kutta法による一階常微分方程式の解法
・ねこ騙し数学 ルンゲ=クッタで連立常微分方程式を解く
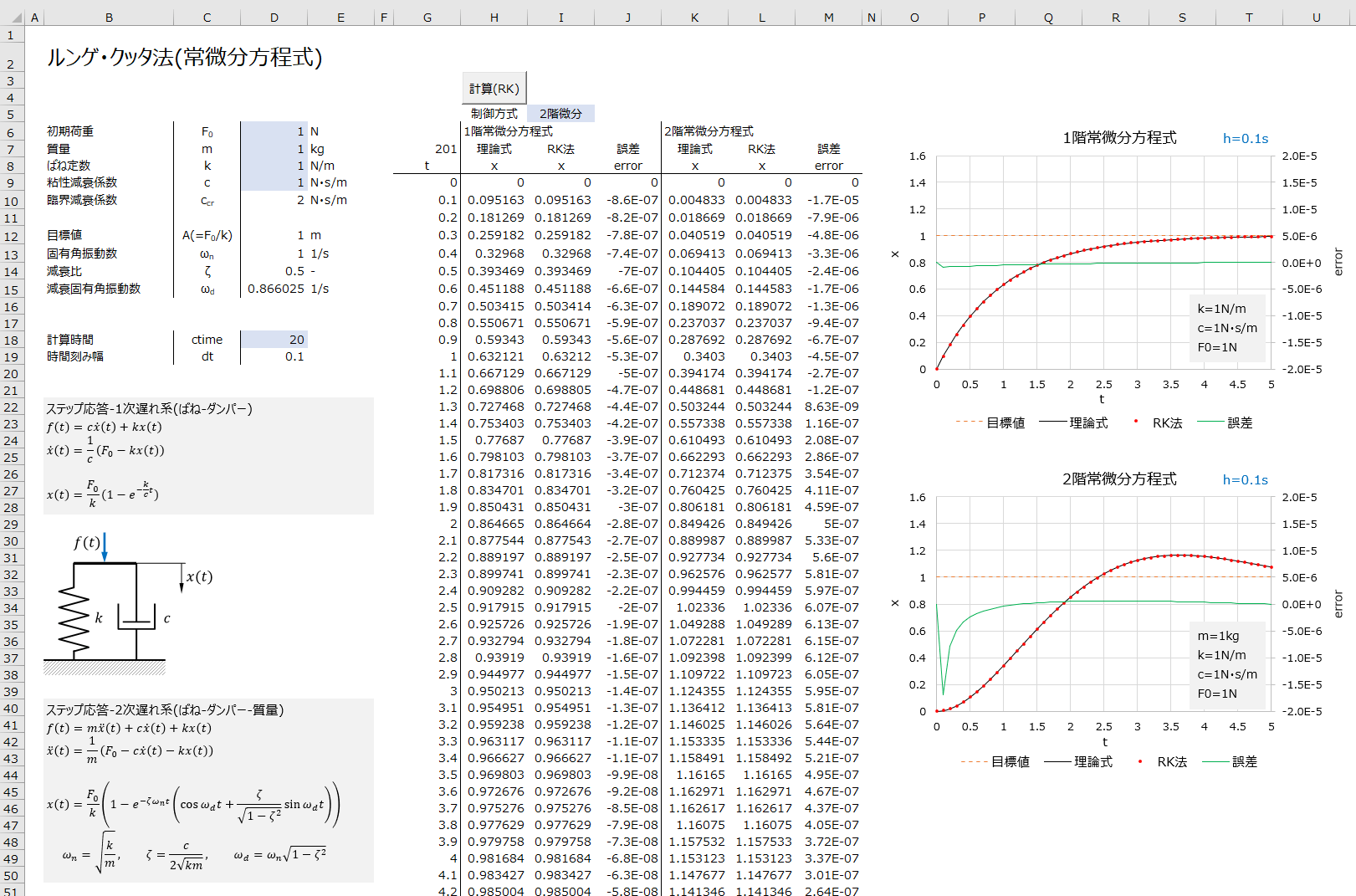
ルンゲ・クッタ法サンプル
記事中で紹介した、過渡応答モデルでのルンゲ・クッタ法の適用例のExcelです。
マクロのコードは、分かり易さを優先して、若干冗長な書き方にしています。
コードにはロックはかけていませんので、自由にアレンジしてみて下さい。
revB以降、ActiveXに関するMicrosoftのポリシー変更に対応するため、マクロ実行ボタンの表示方法を変更しています。
2025.6.14 更新 (revA→revB)
DL解除コード:a602
