べき乗の逆数の和
3,077
|
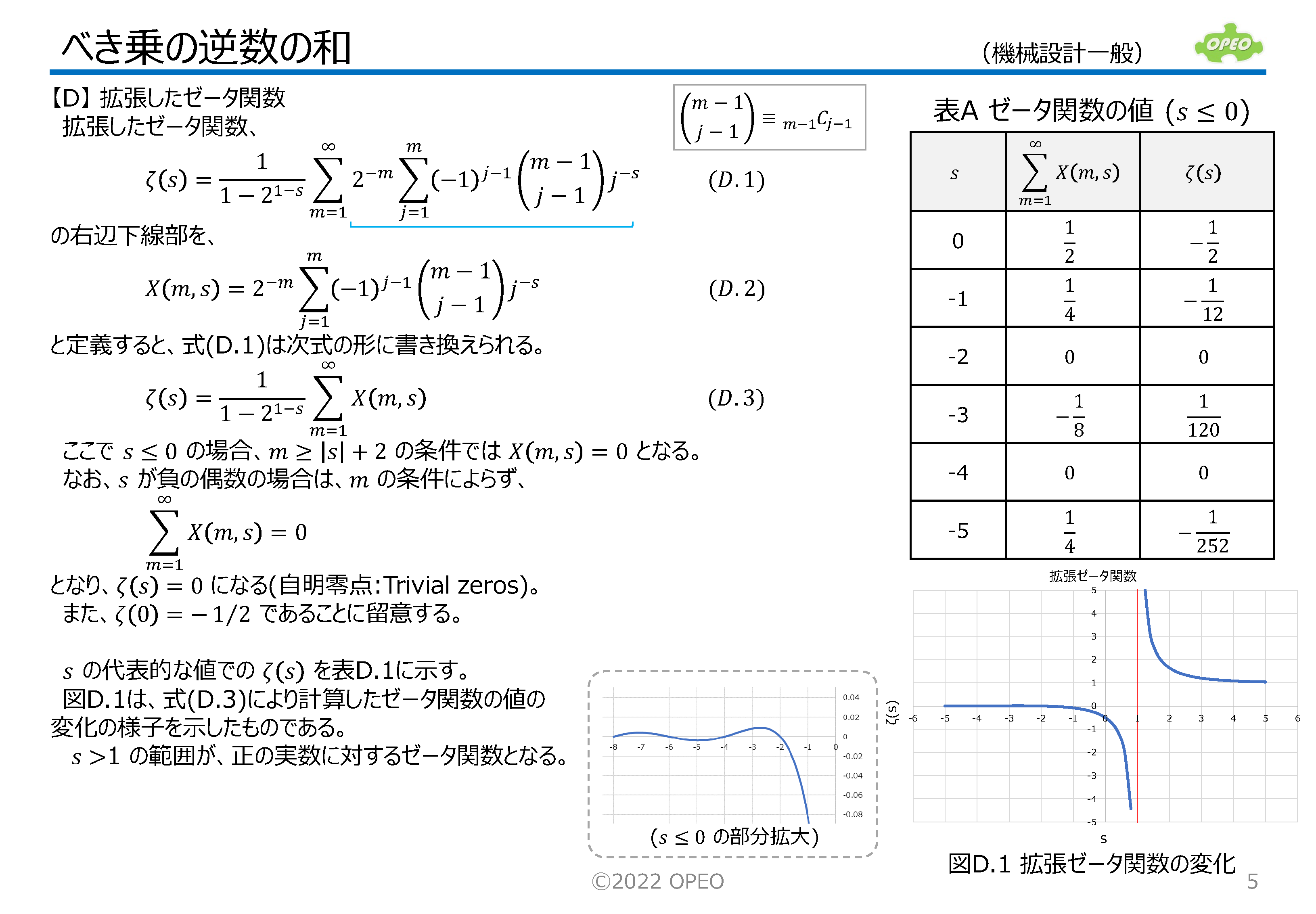
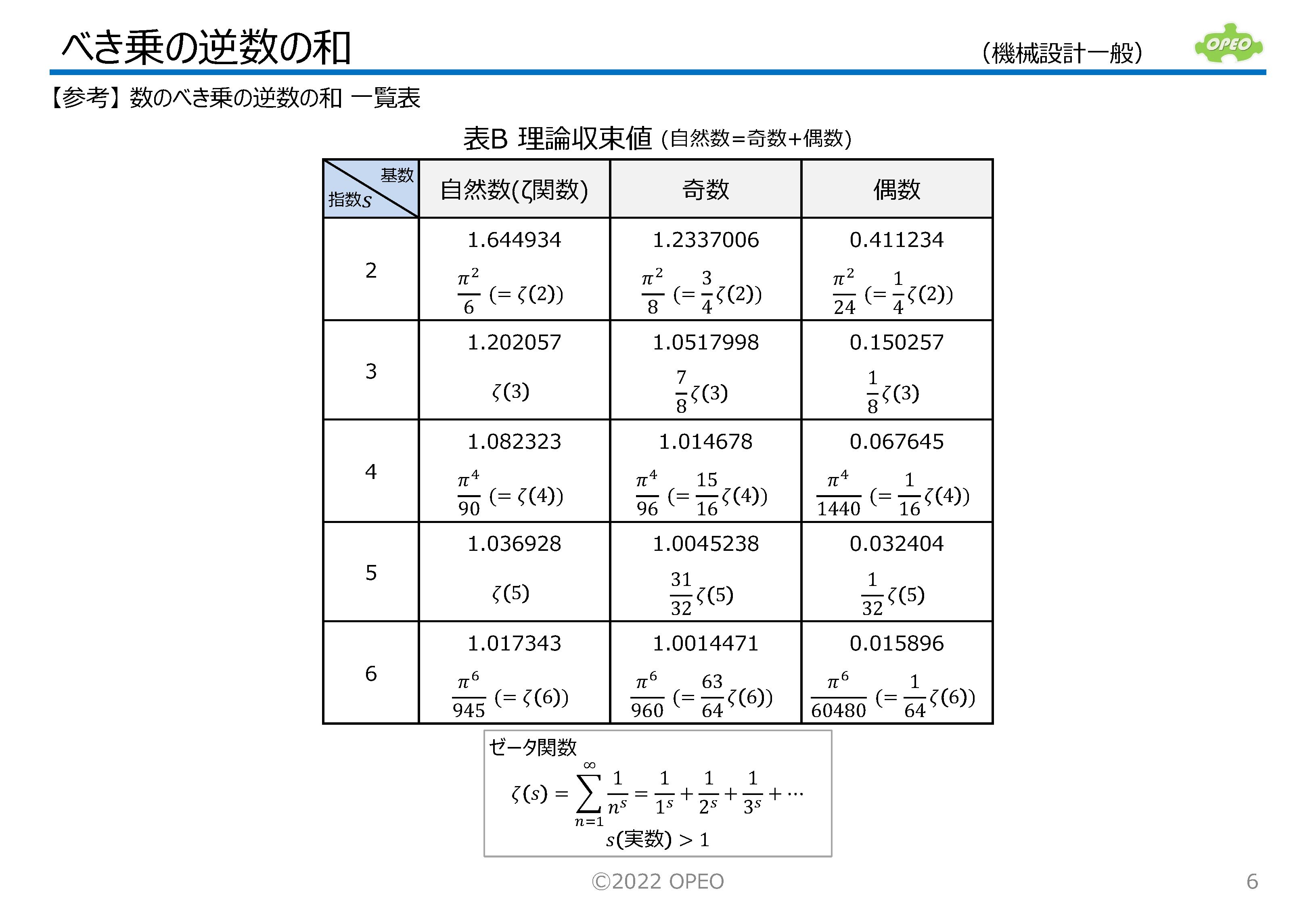
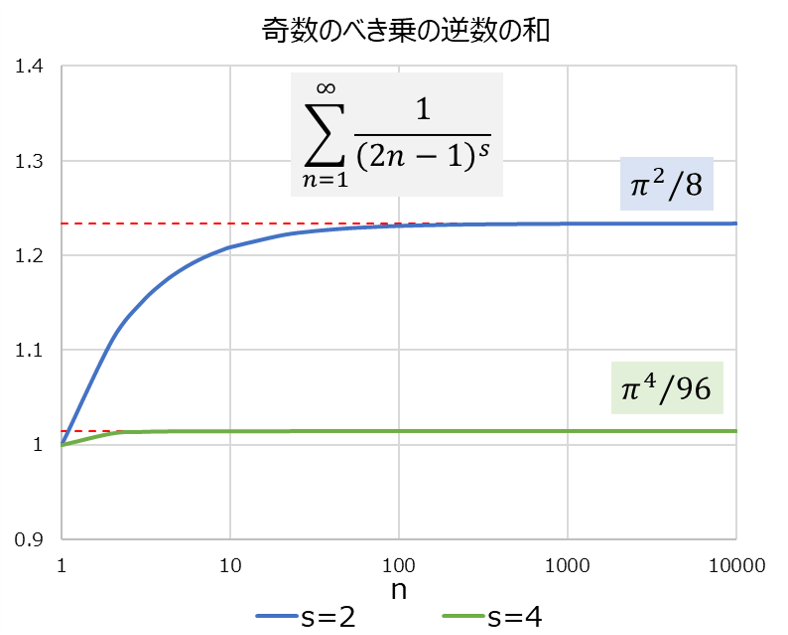
自然数(正の整数)のべき乗の逆数を、数を1つずつ増やして加算する、という計算を極限まで続けると、解がある値に収束するのですが、その一般解(指数を任意の実数に拡張したもの)としてゼータ関数があります。 このような計算は、通常の技術計算の中で登場することはあまりありませんが、分母のべき乗の底が奇数の場合の収束値は、別掲の矩形断面はりのねじりのねじり係数計算に使われるため、導出の過程を理解しておくのもよいでしょう。 ここでは右上の式に示す、奇数を底とし、指数が2と4の場合のべき乗の逆数の和の値を、計算手順を少し工夫することで求める方法について、解説しています。 右下図はこれらが収束していく様子のグラフですが、底と指数の特定の組み合せの場合に、解がπのべき乗を含んだ、非常に簡単な形式で表されることがわかります。 なお、指数が偶数の場合はcos関数、奇数の場合はsin関数のマクローリン展開を用います。 後半に、奇数の交代級数のゼータ関数(拡張されたゼータ関数)に関する式をまとめてあります。 |
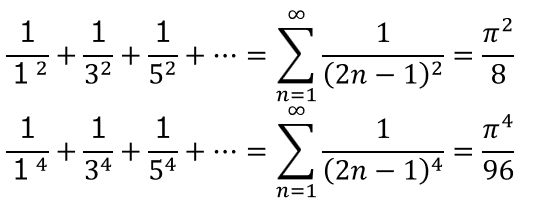 |
 |
<参考URL>
・奇数の2乗の逆数の和
・奇数の4乗の逆数の和
・自然数の累乗の逆数の和-高校数学の基本問題 (級数和の確認用)
・Sin級数にテイラーシステムを適用する (奇数の交代級数のゼータ関数)
・πとの関連性 (交代級数の考察)
・解析接続したゼータ関数, ζ(0), ζ(-1), ζ(-2)の値 (拡張したゼータ関数の定義式)
・Particular values of the Riemann zeta function (ゼータ関数の特殊値)
・Riemann のゼータ関数 (ゼータ関数の基本理論とグラフ例)