ヘルツの弾性接触
34,268
|
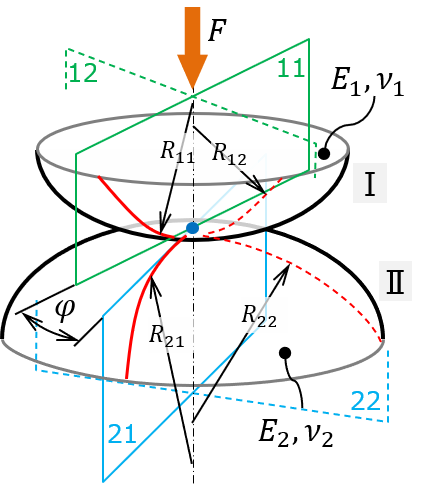
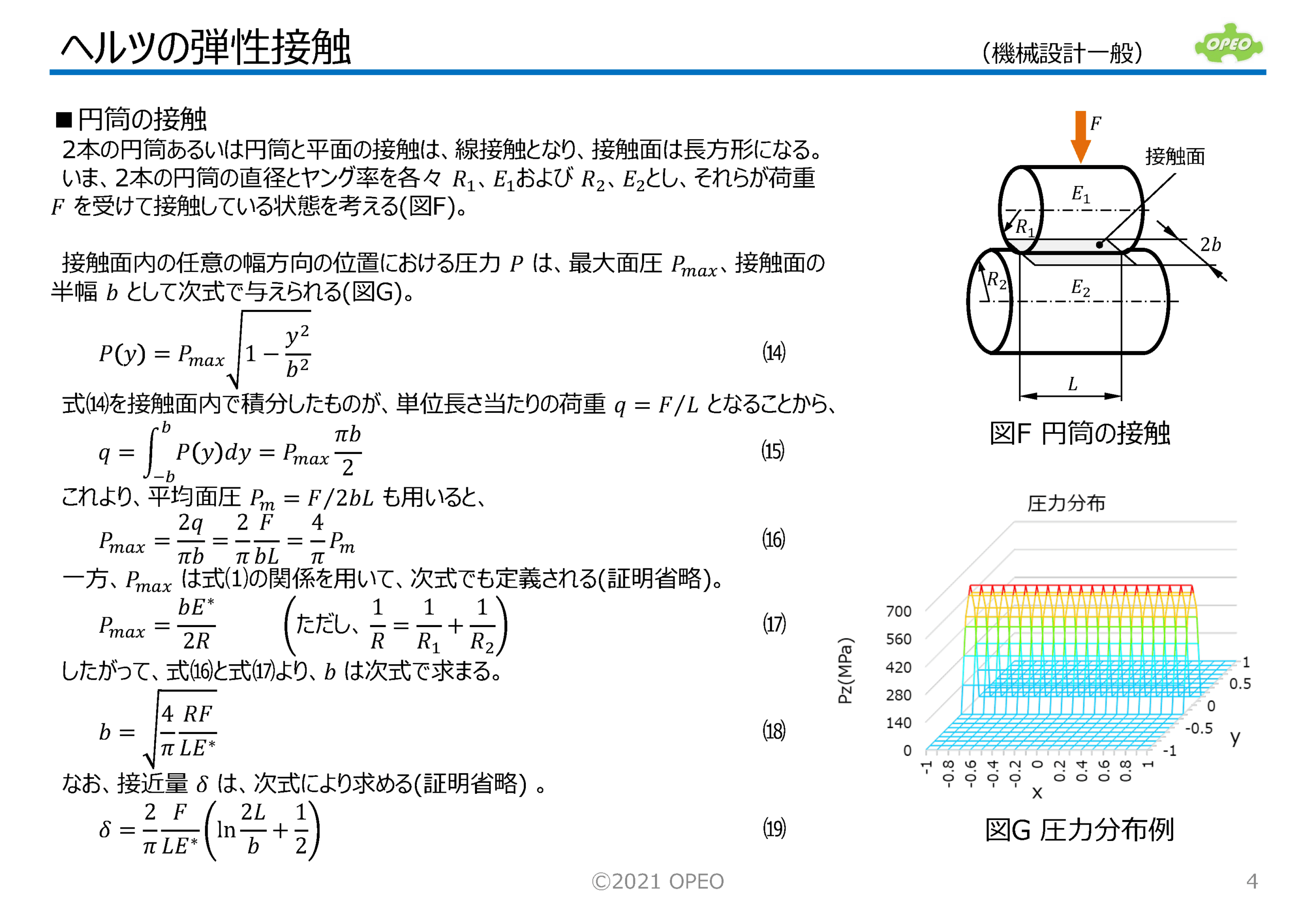
ヘルツの弾性接触理論は、2つの物体(固体弾性体)の間にすべりや摩擦が生じないと仮定した場合の、弾性範囲内での接触変形に関する理論で、現在に至るまで弾性接触のバイブル的な存在でもあります。 なにぶん歴史の古い理論のため、数式に用いられている記号や表現方法も、資料によって色々なパターンがありますが、この記事ではできるだけ統一された体裁となるよう編集してあります。 なお、円筒面の接触に関しては、ヘルツの理論ではなく、JohnsonやPuttockらの研究結果を参照しています。 最後に、Excelでの計算シートと原著の対訳も公開しています。 |
 |
|
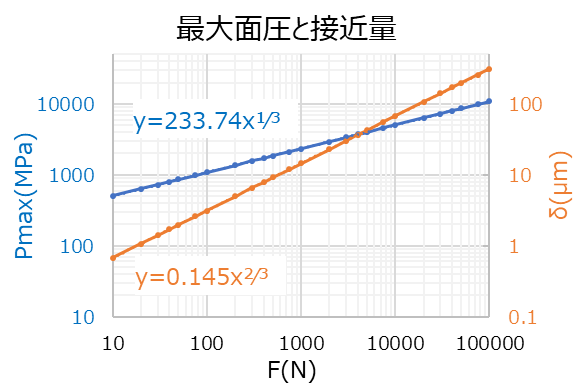
ちなみに、荷重(F)をパラメータとして、最大面圧(Pmax)と接近量(δ)をプロットすると、右図のように両対数上で直線関係にあることがわかります。 |
 |
<参考文献>
・金多 潔他(1973), “弾性論(第3版)”, コロナ社, p.429-434
(原著：Timoshenko,S.P, Goodier,J.N(1970), “Theory of Elasticity Third edition“, McGraw-Hill
・Johnson.K.L(1985), “Contact mechanics”, Cambridge university press
・Puttock.M.J,Thwaite.E.G(1969), “Elastic Compression of Spheres and Cylinders at Point and Line Contact”, National Standards Laboratory Technical Paper No.25
<参考URL>
■理論
・ヘルツの接触理論-技術計算製作所
・Hertzian contact equations for elliptical, spherical and cylindrical contacts-TriboNet
・岡本純三(2011), “ボールベアリング設計計算入門”(二物体の接触), 日刊工業新聞社
・公式集03-2_ヘルツの式(球の接触)-機械設計技術者
■論文原著
・https://home.uni-leipzig.de/pwm/web/download/Hertz1881.pdf
・https://digbib.ubka.uni-karlsruhe.de/volltexte/digital/1/215.pdf (ヘルツ論文集の一部)
■計算関連
・接触応力の計算-MESYS (検算のために利用)
・接触面圧計算-技術計算製作所 (検算のために利用)
・PrecisionMindset (検算のために利用)
・二重指数関数型数値積分-シキノート
ヘルツの弾性接触計算Excel
ヘルツの弾性接触のExcel計算シートです。
(楕円関数の計算に用いている、二重指数関数型数値積分には、シキノートさんのサイトの記事とソースコードを参考にさせていただきました)
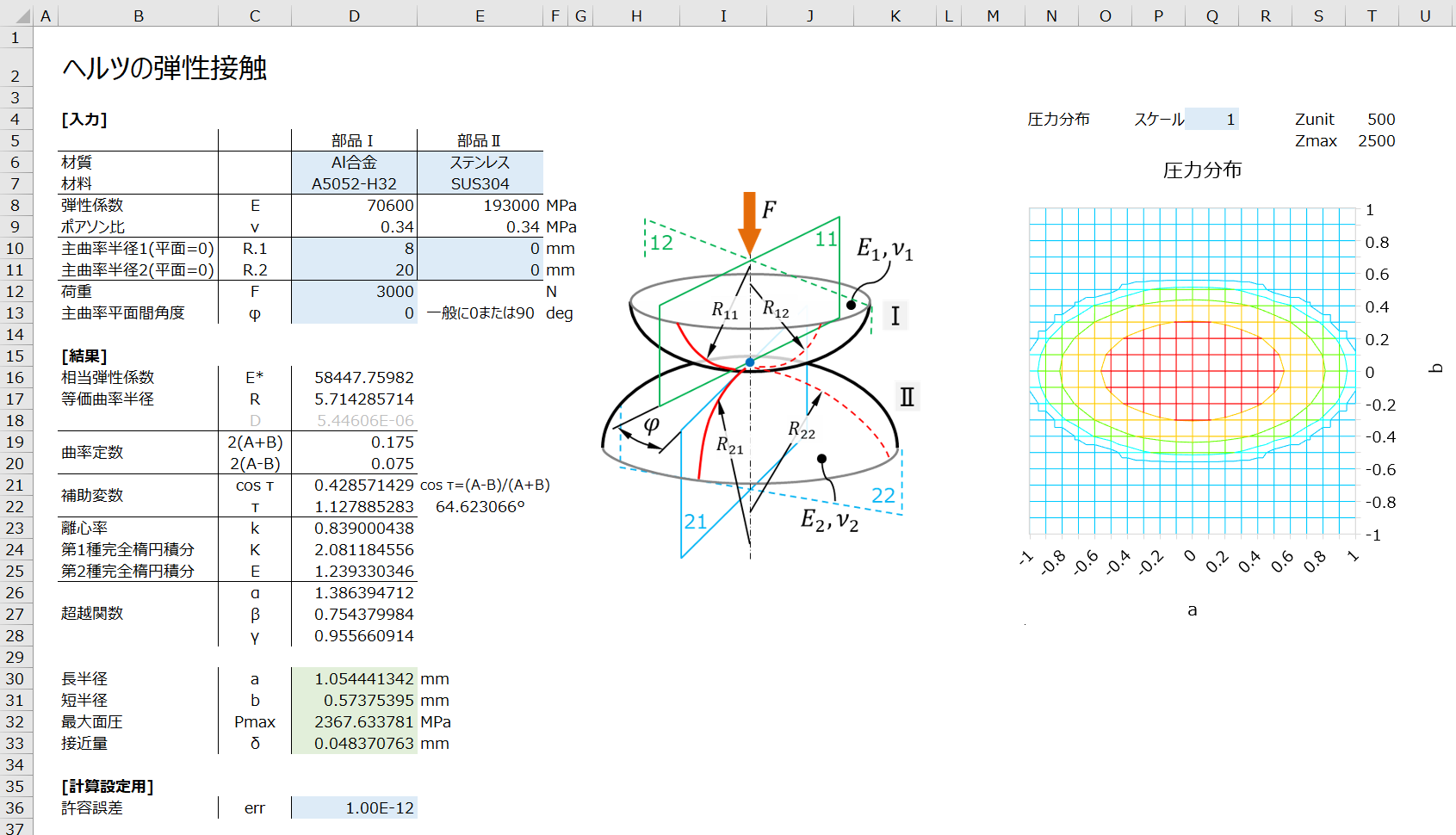
球面を含む楕円放物面、平面および円筒面の場合の接触計算を行ないます。
2つの主曲率半径は、正で凸面、負で凹面、またどちらかが0で円筒面、両方とも0で平面として計算します(それ以外は楕円放物面)。
<更新履歴>
・revF：材質と材料をプルダウンメニューから選択すると、対応した物性値をセットします(材料データシートはカスタマイズ可能)。
・revG：円筒の接触計算に対応しました。
収束計算(反復計算)のロジックを変更(二分法→改良版セカント法)しました。
また、簡易的なグラフ表示設定も可能にしました。
なお、Excelは2019で作成していますので、それ以前のバージョンでは正常に動作しない可能性がありますことを、予めご了解願います。
2025.8.25 更新 (revF3→revG)
固体弾性体の接触について(H.Hertz)
Hertzの弾性接触に関する論文(独語)の対訳です。
この論文の一部を引用した文献や記事は多いのですが、実際ヘルツ氏がどのような文章を書いていたのかを理解するために、和訳に取り組みました。
生成AIによる翻訳結果を少し手直ししたものですので、あくまでも参考程度にして下さい。
(なお、この二次的著作物を含む論文の著作権に関しては、原著者であるHertz氏の没後70年は優に超えており特に問題はないと判断していますが、もし問題ありということであればご指摘いただければ幸いです)
なお、文中で曲率の添字に、文脈上誤植（←ρ12がρ21となっている）と思われる箇所があり(p4)、赤字で変更してあります。
この論文では、弾性体どうしの微小接触領域で発生する物理現象の理論的解説を延々と行ったのち、最後はなんと、地球サイズの鋼球が接触するとどんなことが起こるか、という考察で締めくくられています。
<更新履歴>
・revE：和訳内容を全面的に見直しました。
★ 2024.8.30 より、本資料は公開パスワード方式に変更しました。
〔サンプル画像〕
2025.8.18 更新 (revE→revE1)
DL解除コード：a507
