不静定次数の計算
106
|
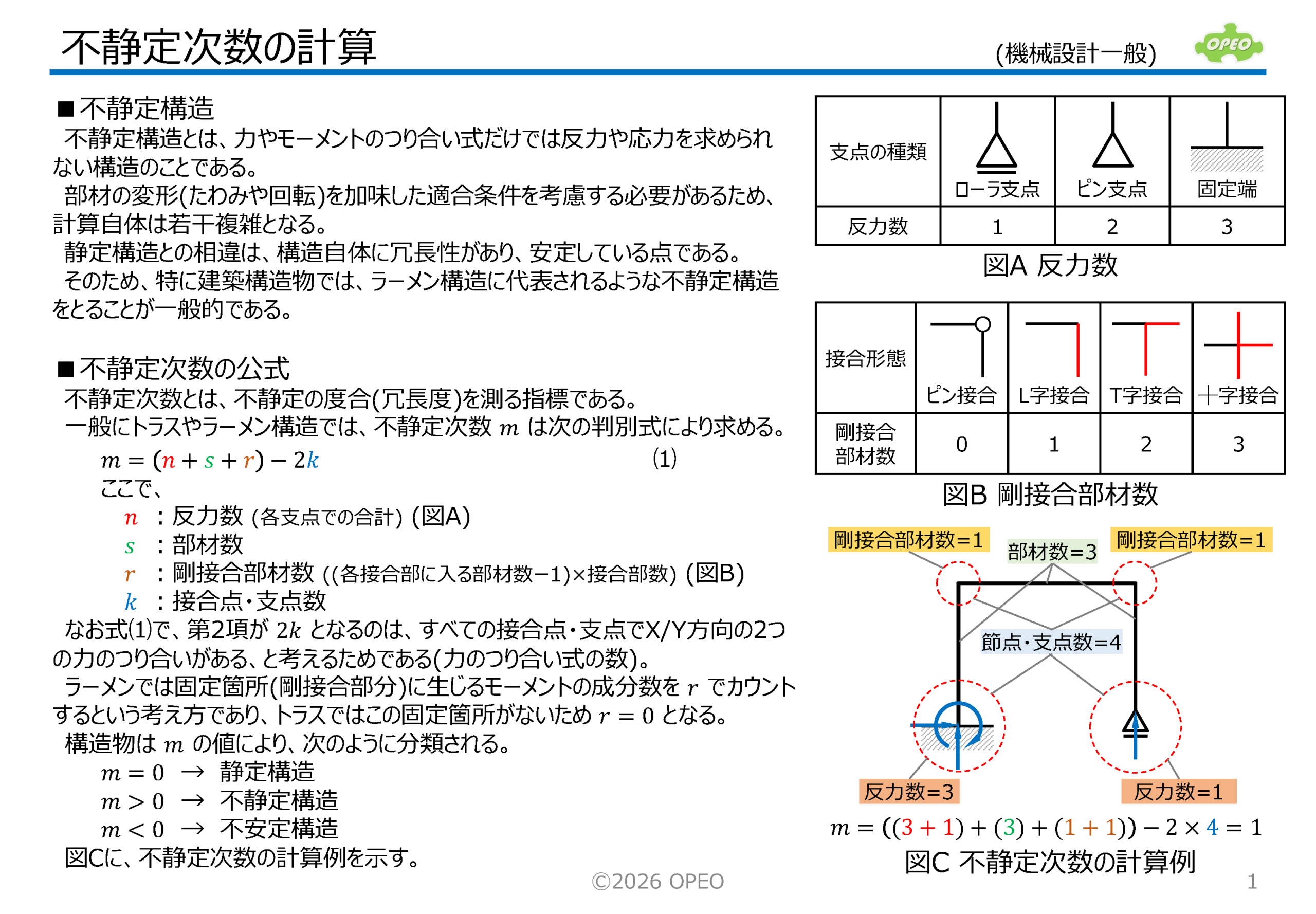
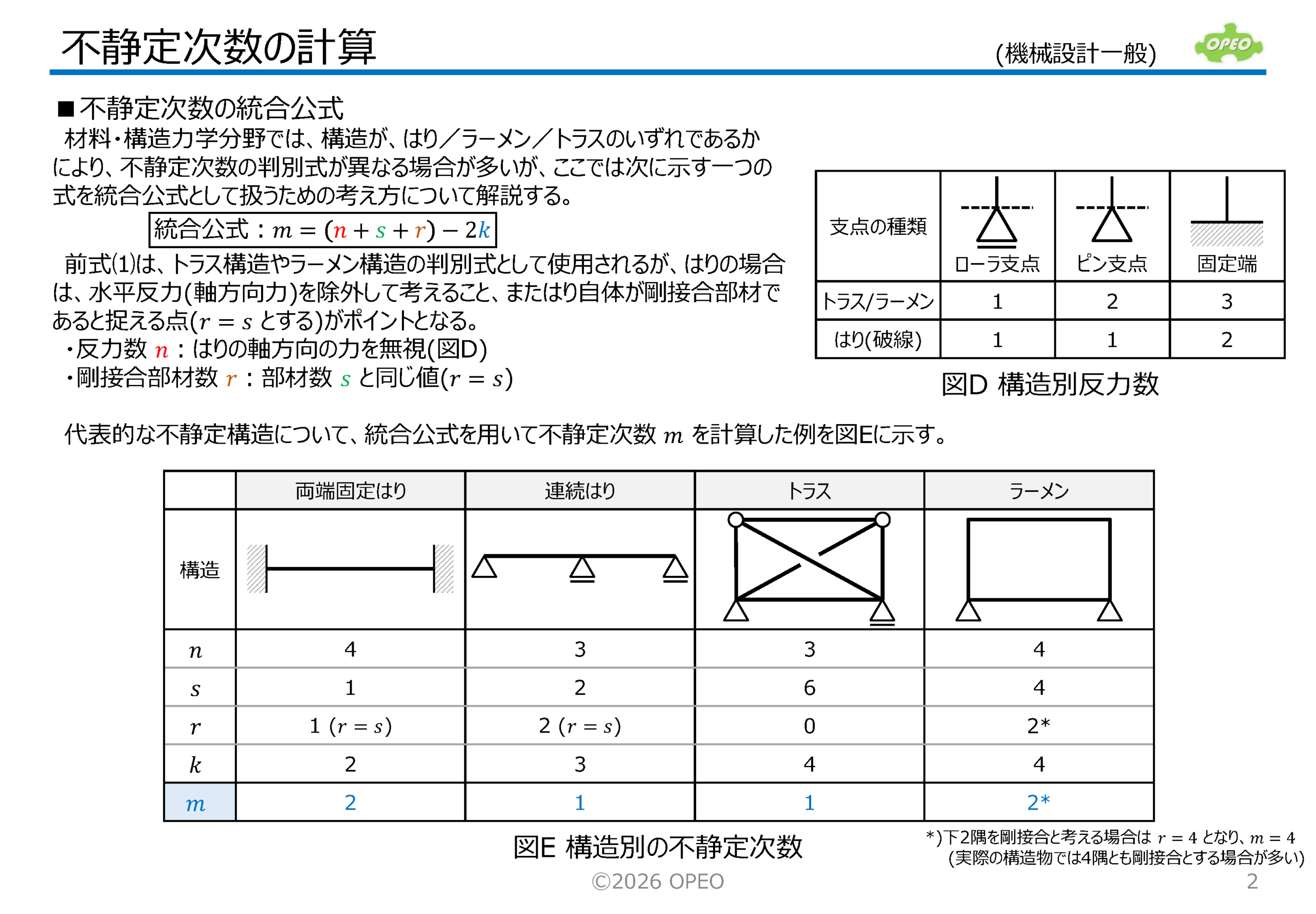
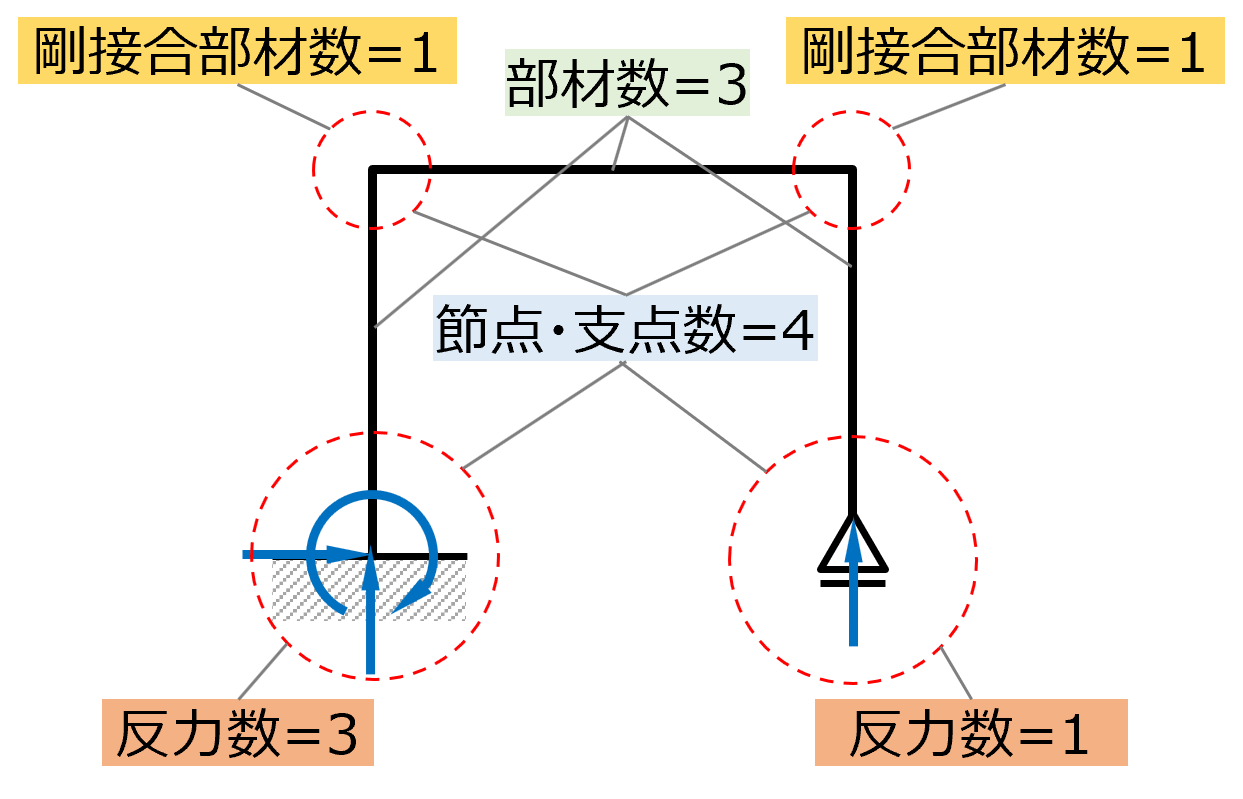
不静定構造の不静定次数を算出する、統合公式についての解説です。 不静定構造とは、力やモーメントのつり合い式だけでは反力や応力を求められない構造のことで、静定構造との違いは、構造自体に冗長性があり安定している点です。 不静定次数の計算では、一般に、構造がはりかトラスかラーメンかで公式が異なります*が、これらをひとつの統合公式として扱うことができれば便利です。 ここでは、その統合公式と、統合化のために留意すべき点を解説しています。 *) 公式の違い (記号 n, s, r, k の意味については本文参照) |
|