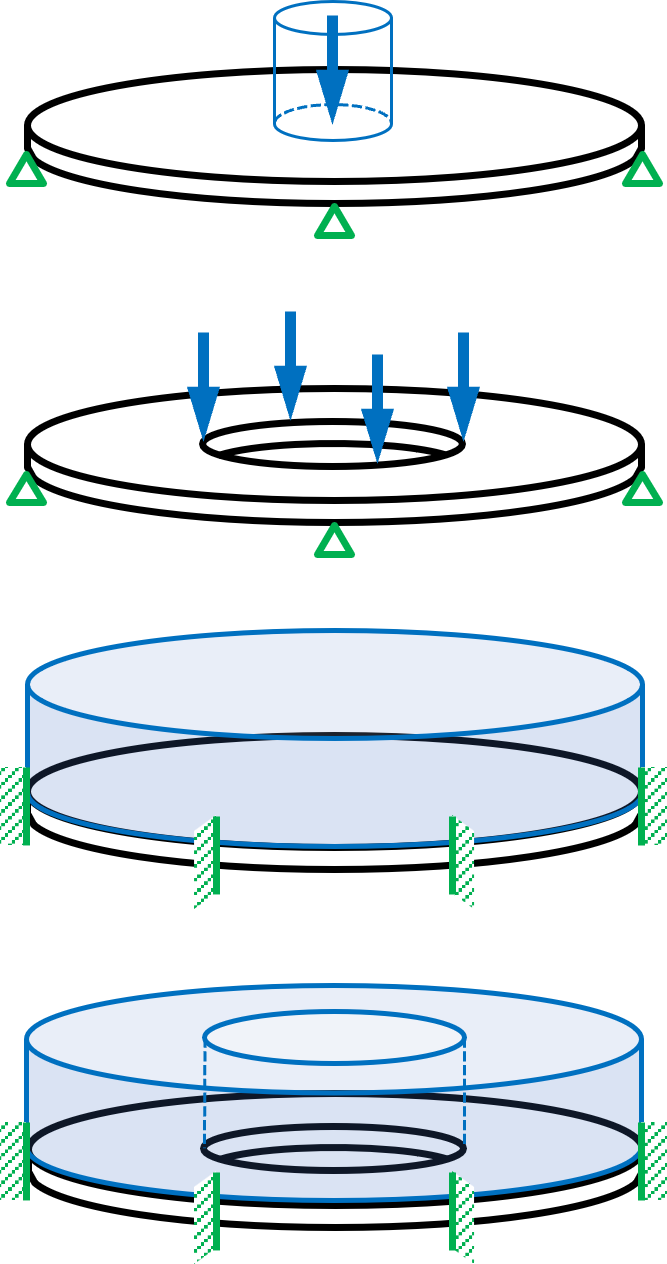
円板のたわみと応力
24,239
|
集中荷重や等分布荷重を受ける、円板のたわみと応力を求める式を集めた資料です。 円板のたわみと応力の計算式はいろいろなサイトで公開されていますが、記事によって式や結果が異なっているケースもあり、どれが正解かわかりにくいという状況もあります。 この記事では、参考文献に掲載されている式を参照して、できるだけ分かり易い形式になるよう式変形した形でまとめています。 ※補足 |
荷重タイプの例 |
<参考文献>
・Young.W,Budynas.R (2020),”Roark’s Formulas For Stress And Strain,9th edition”,McGraw-Hill
<参考URL>
・Roymech – Loaded Flat Plates
・CHAPTER 7 CIRCULAR PLATES AND DIAPHRAGMS. Summary
・オメガエンジニアリング 円板型ダイヤフラムと計算式
・HEISHIN 技術データ集 円板の最大応力と最大たわみ
・Engineers edge “Circular plate deflection calculator” (検算用)
・Circular flat plates calculators (検算用)
・計算サイト 円板変形(全周支持、等分布荷重) (検算用)
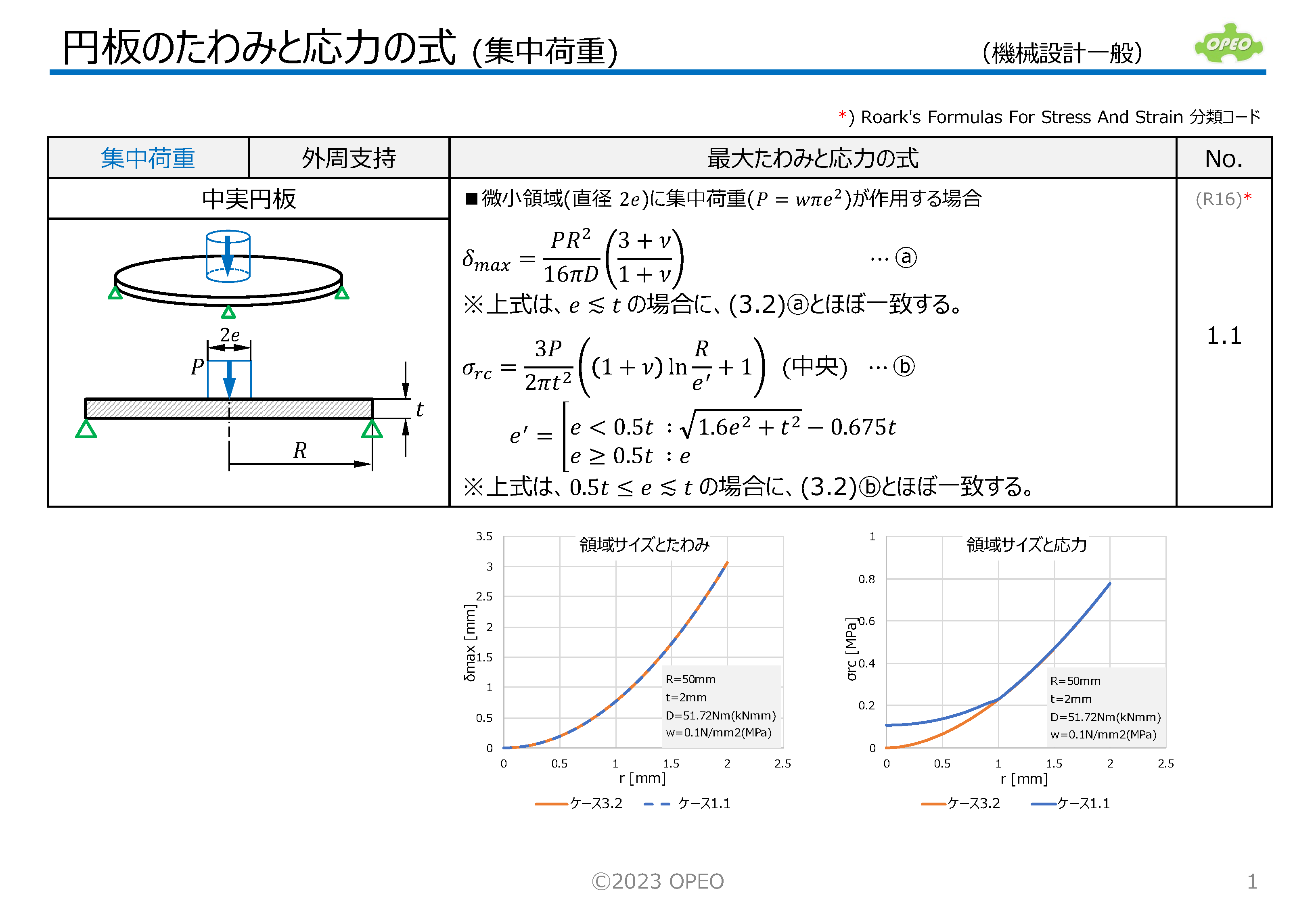
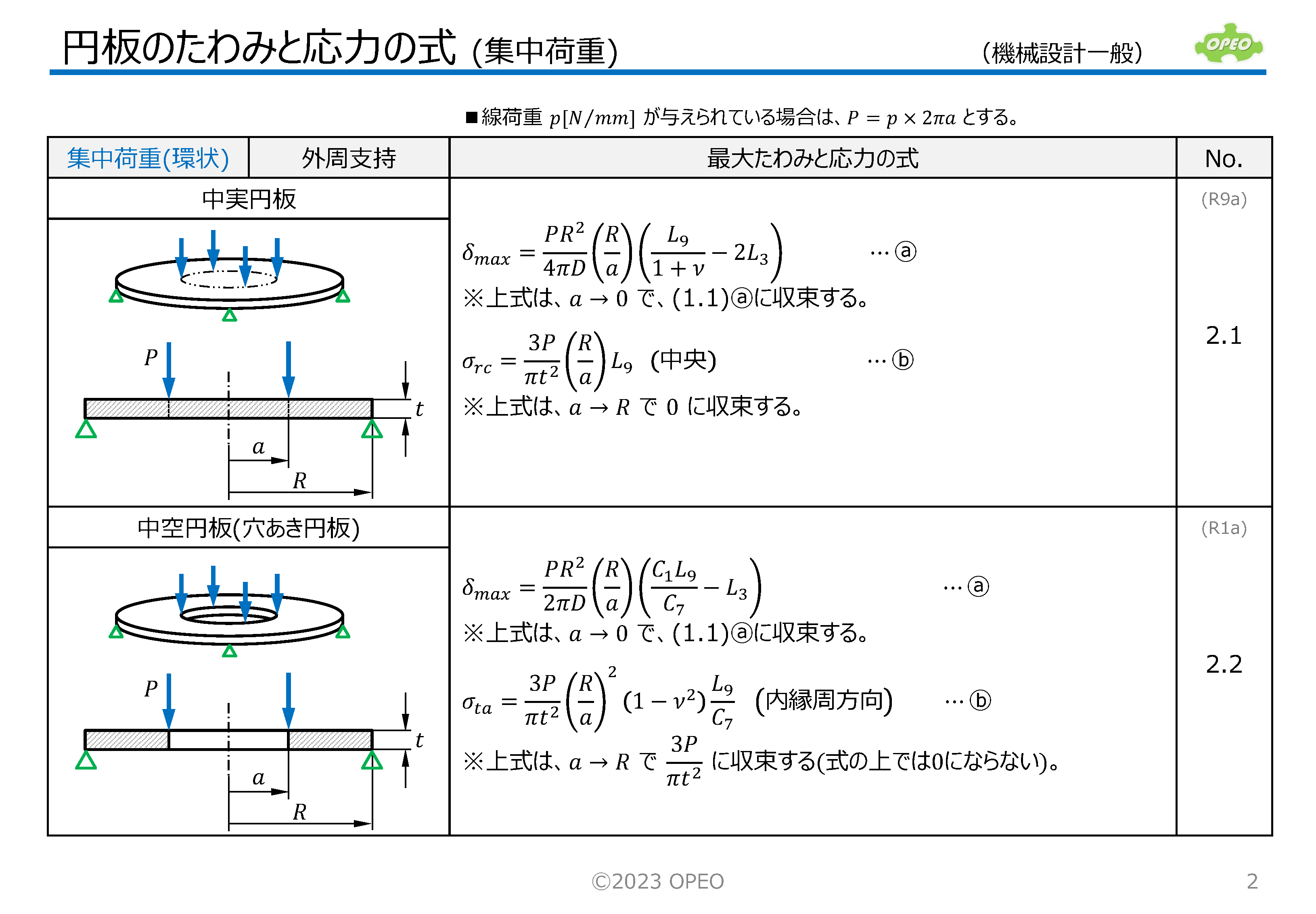
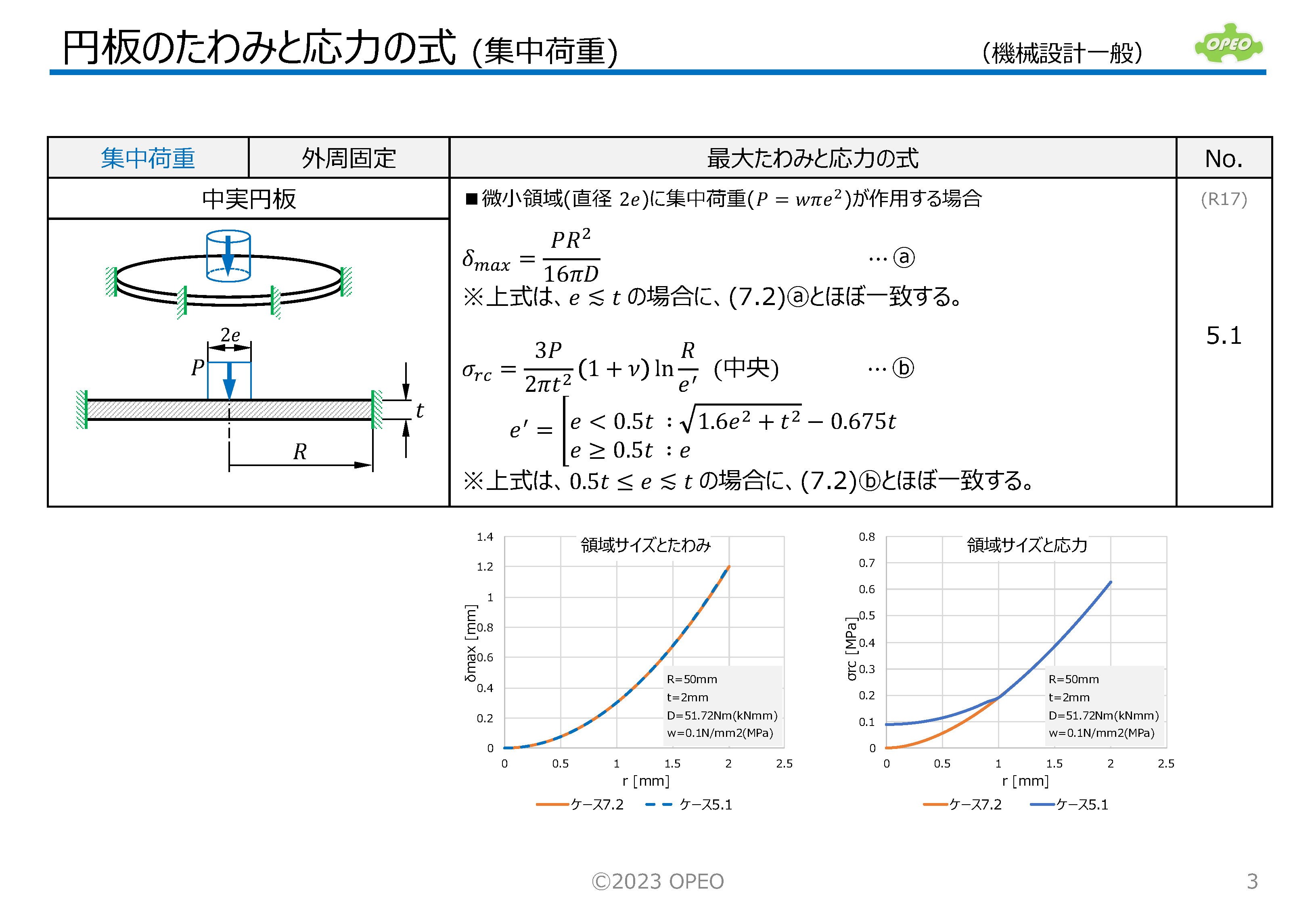
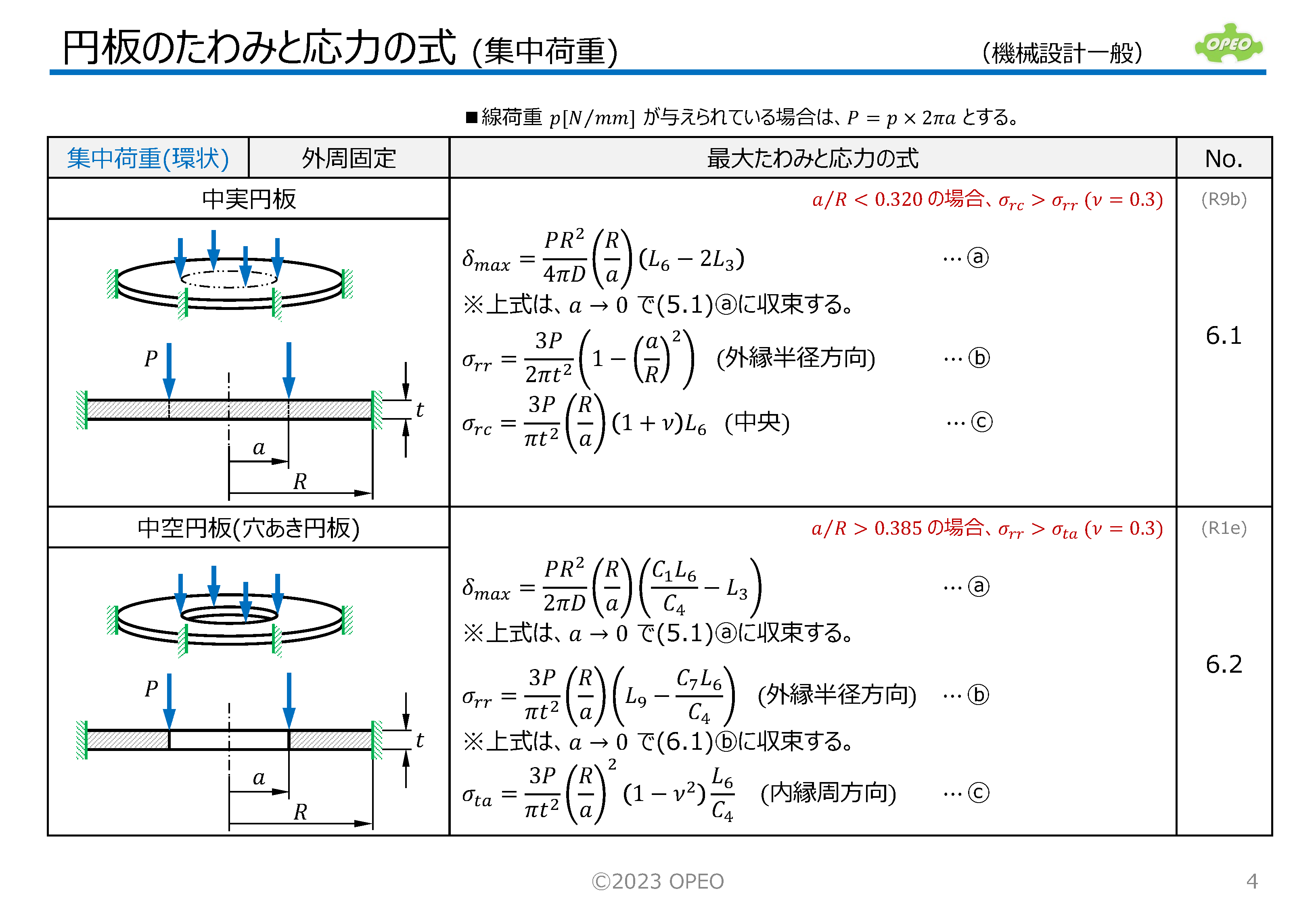
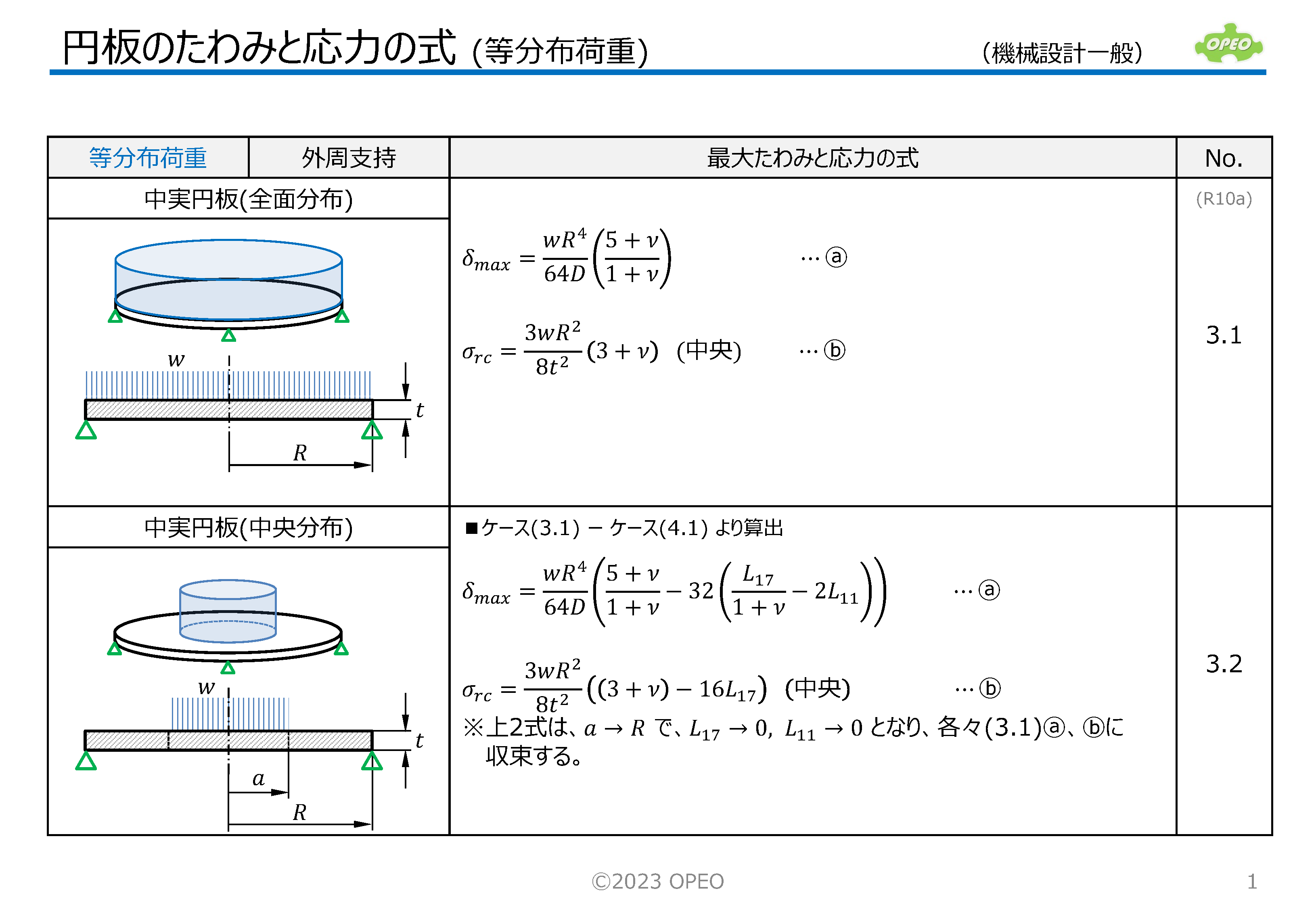
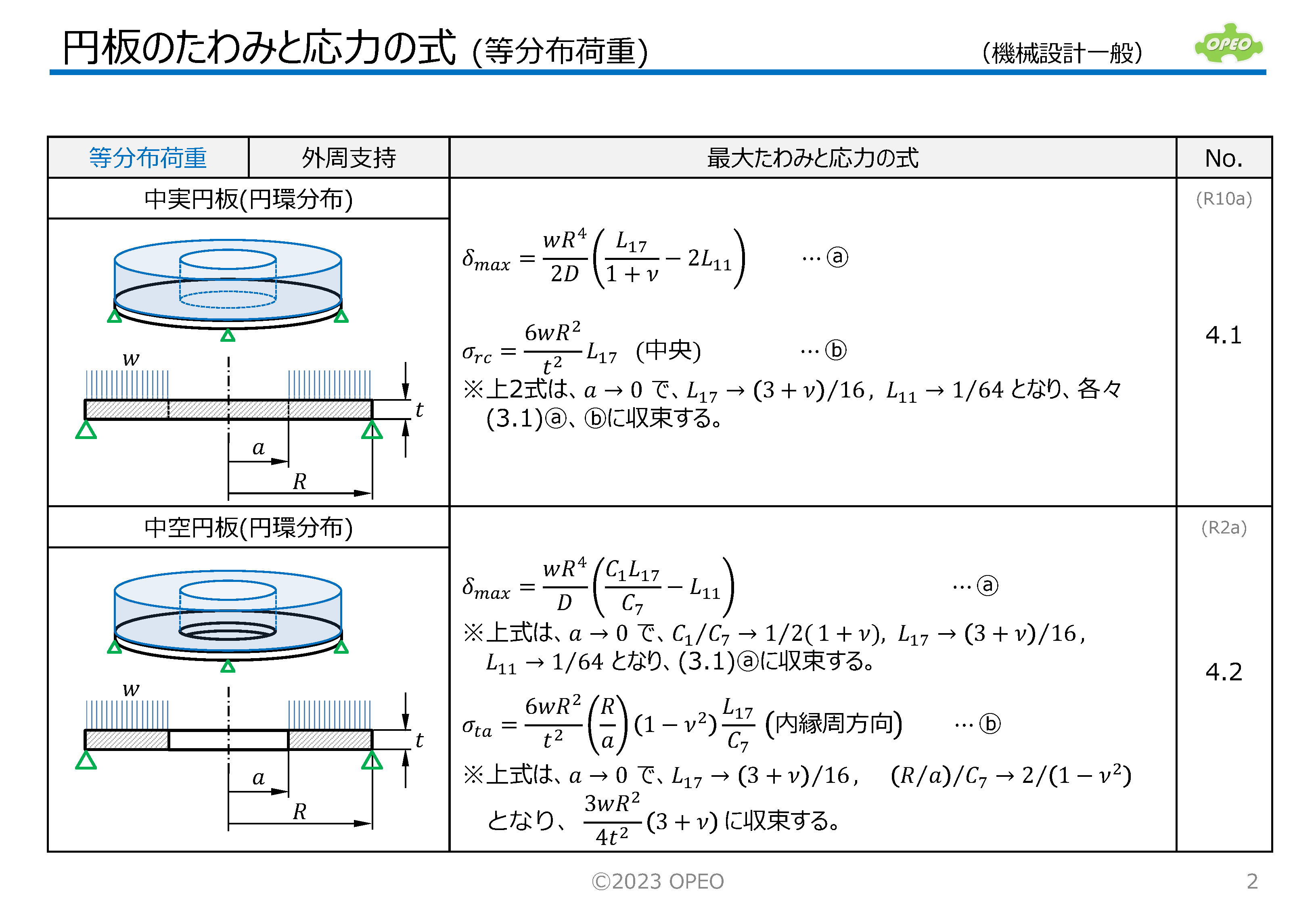
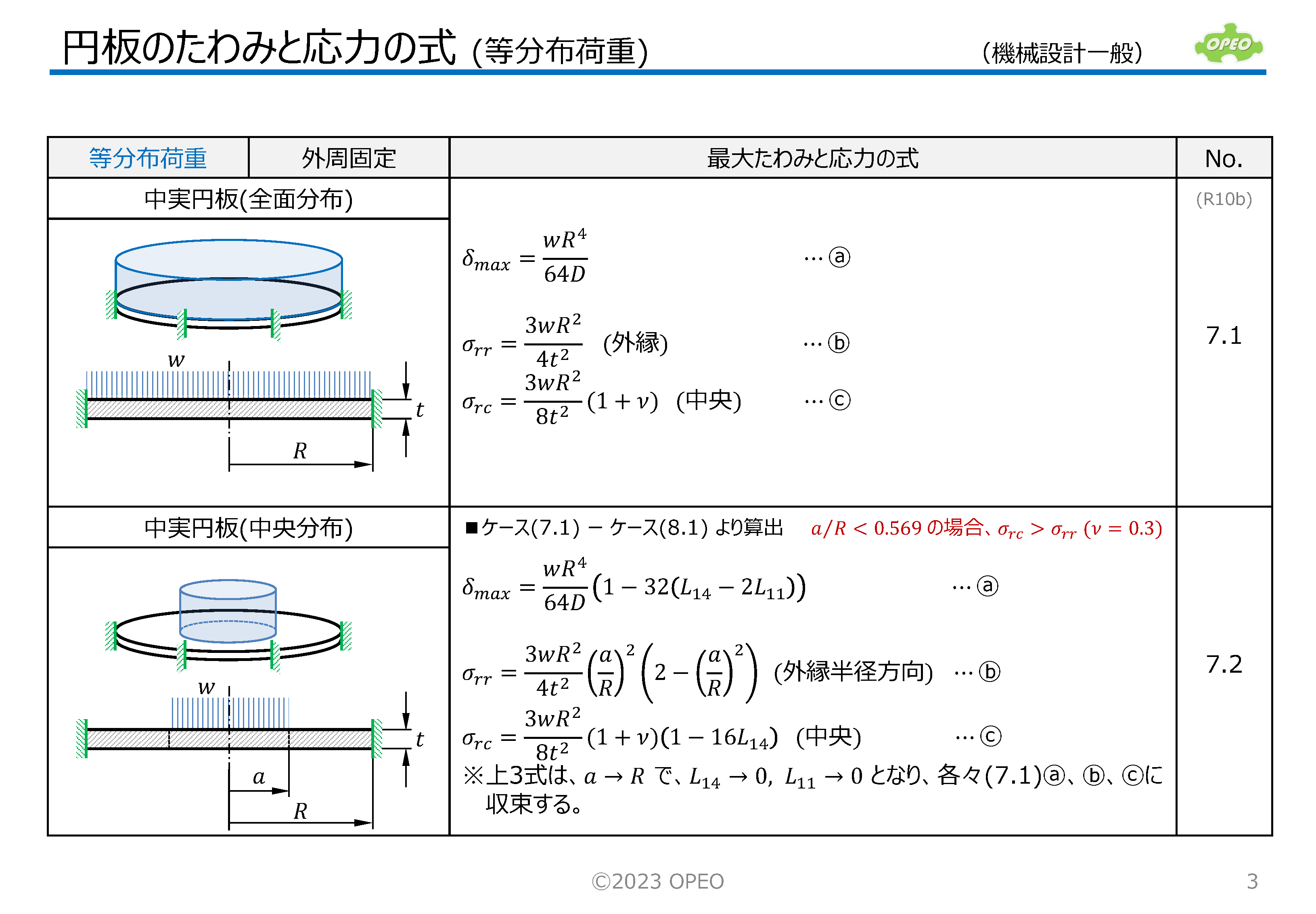
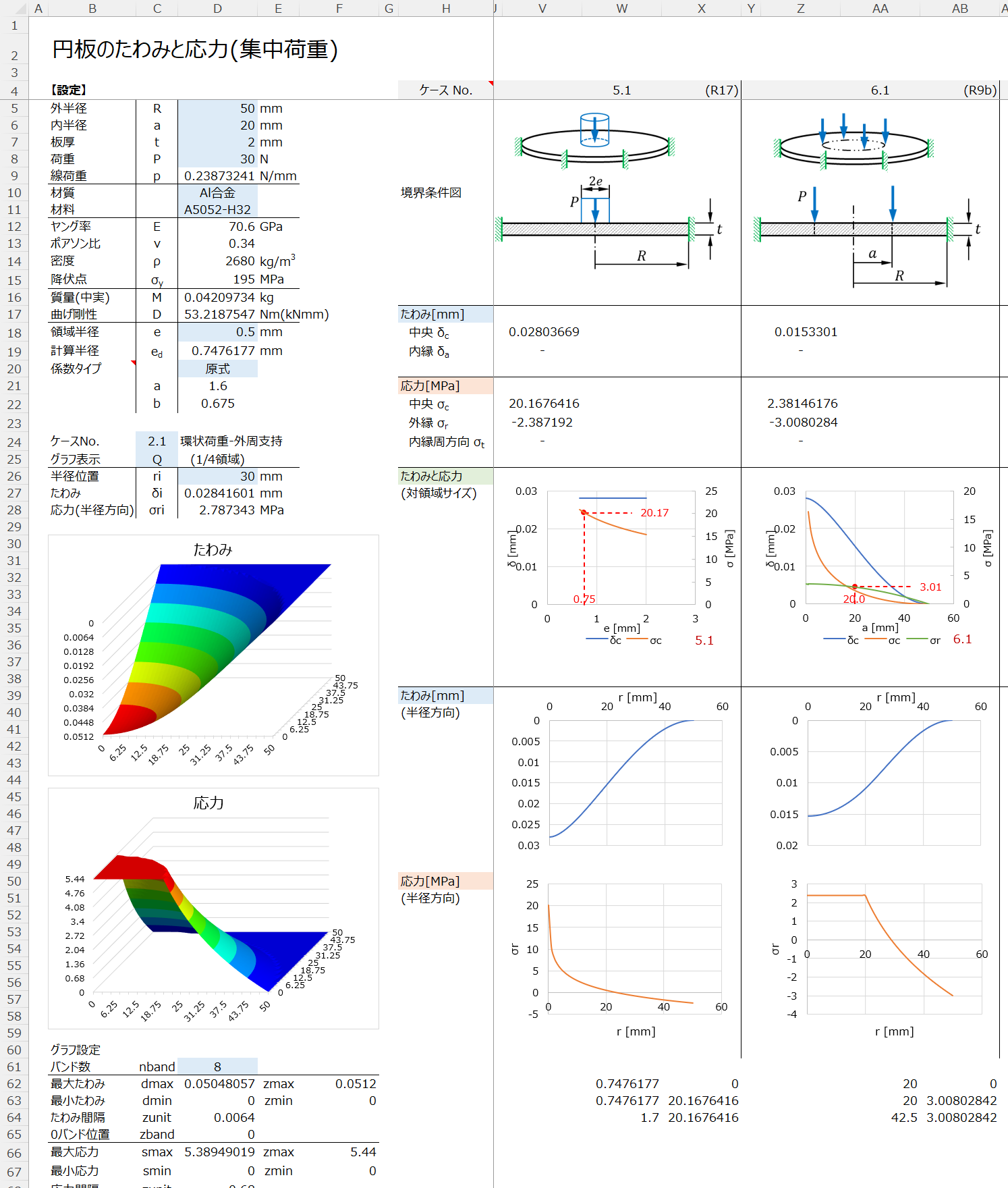
円板のたわみと応力の計算Excel
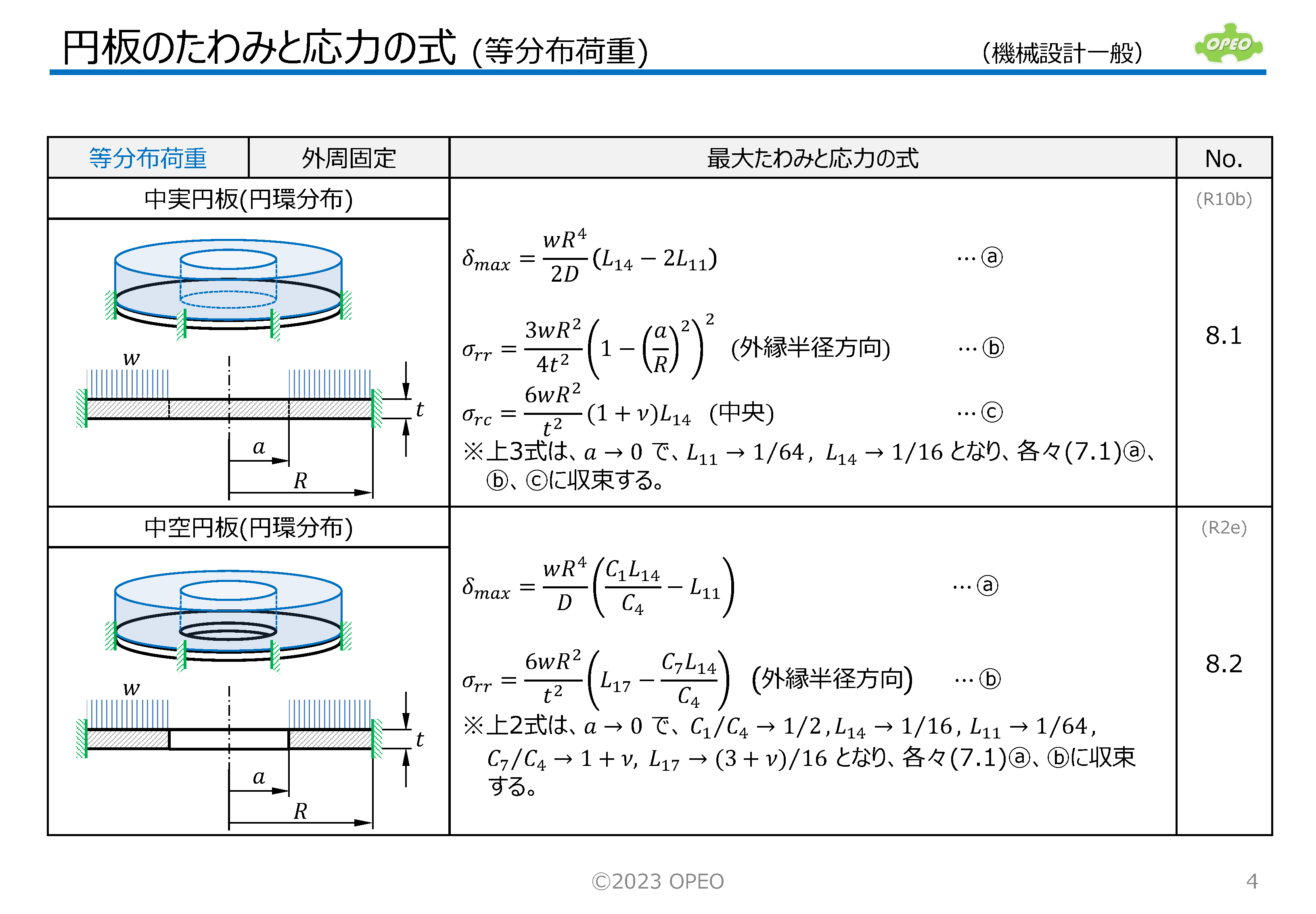
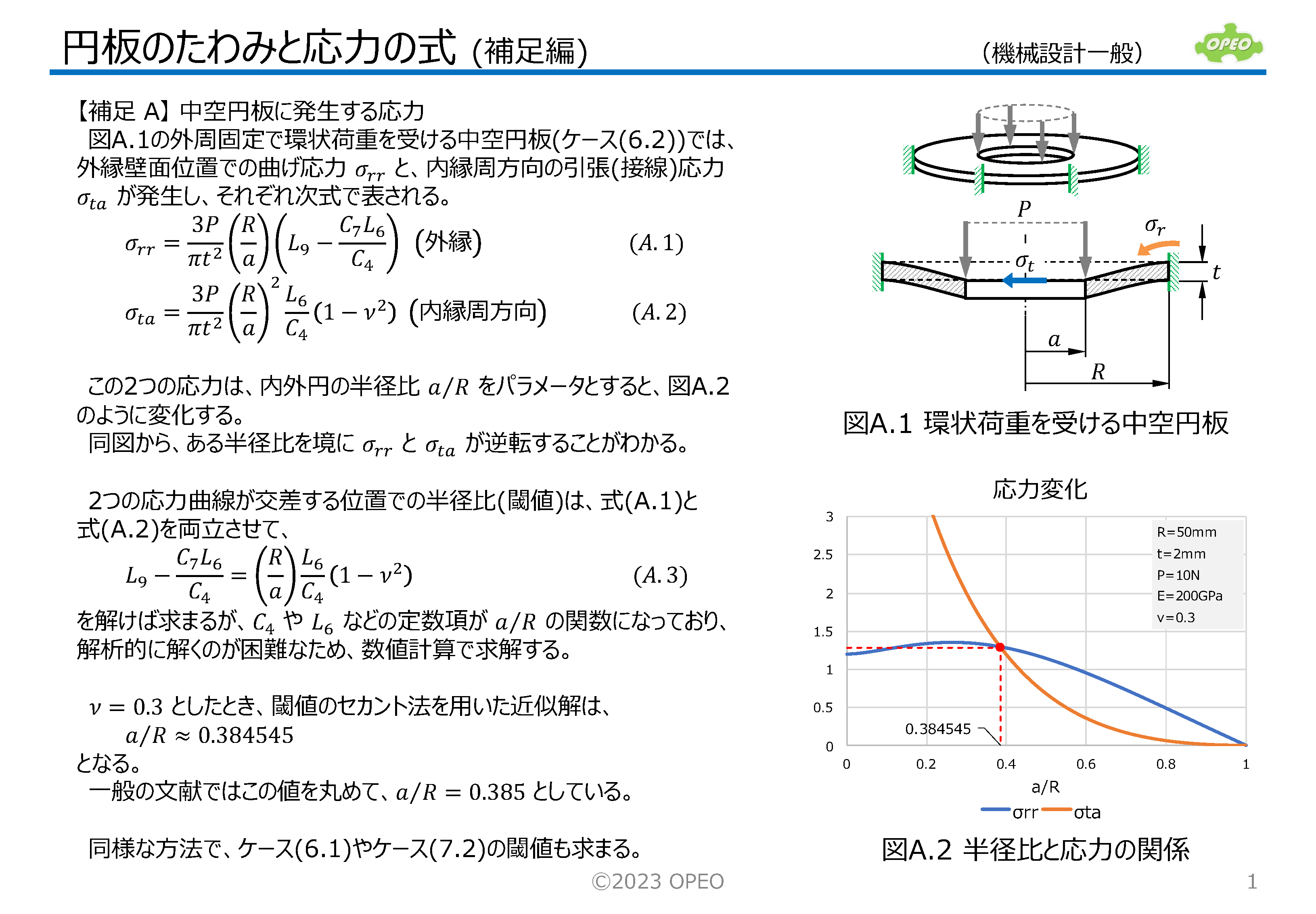
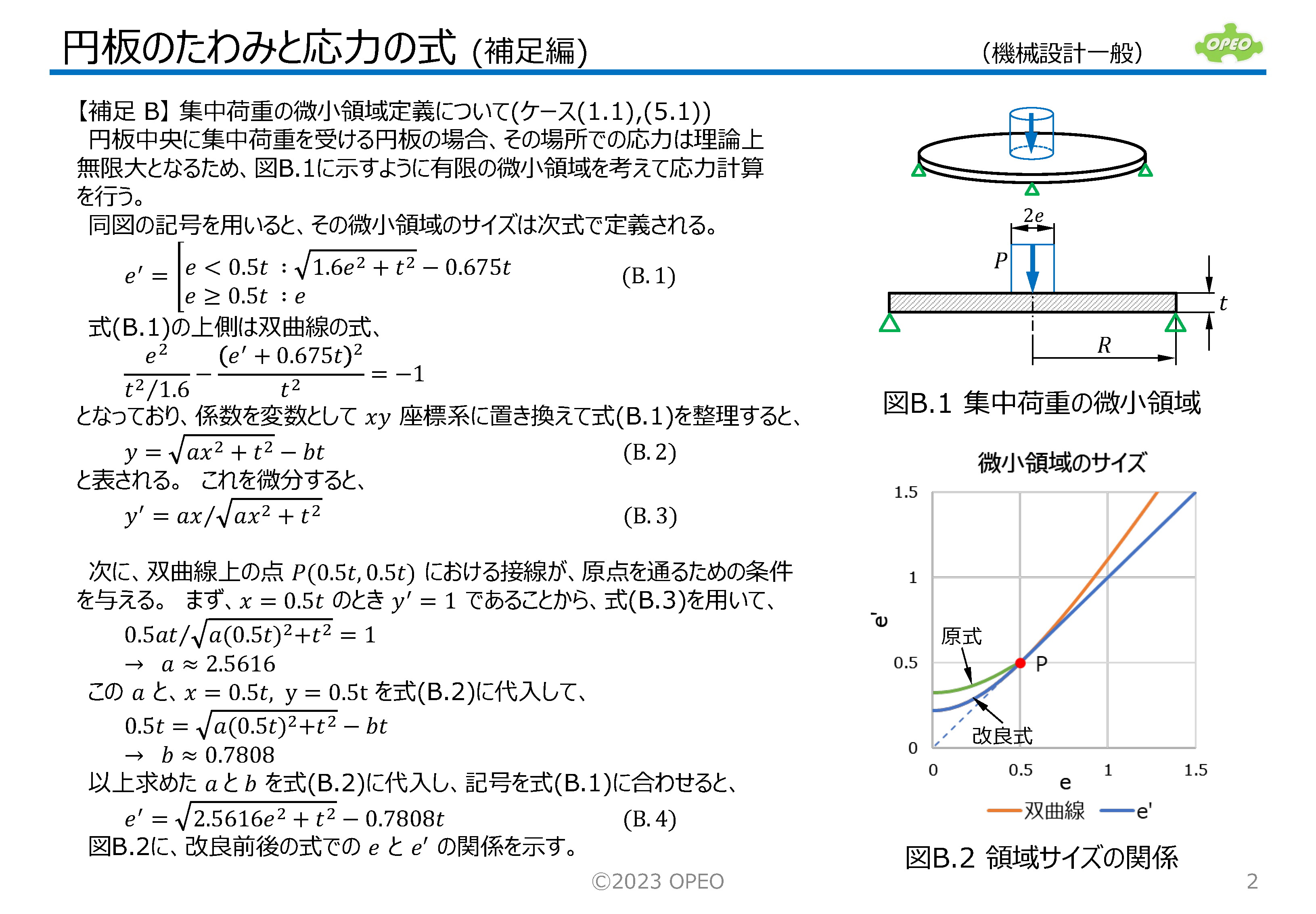
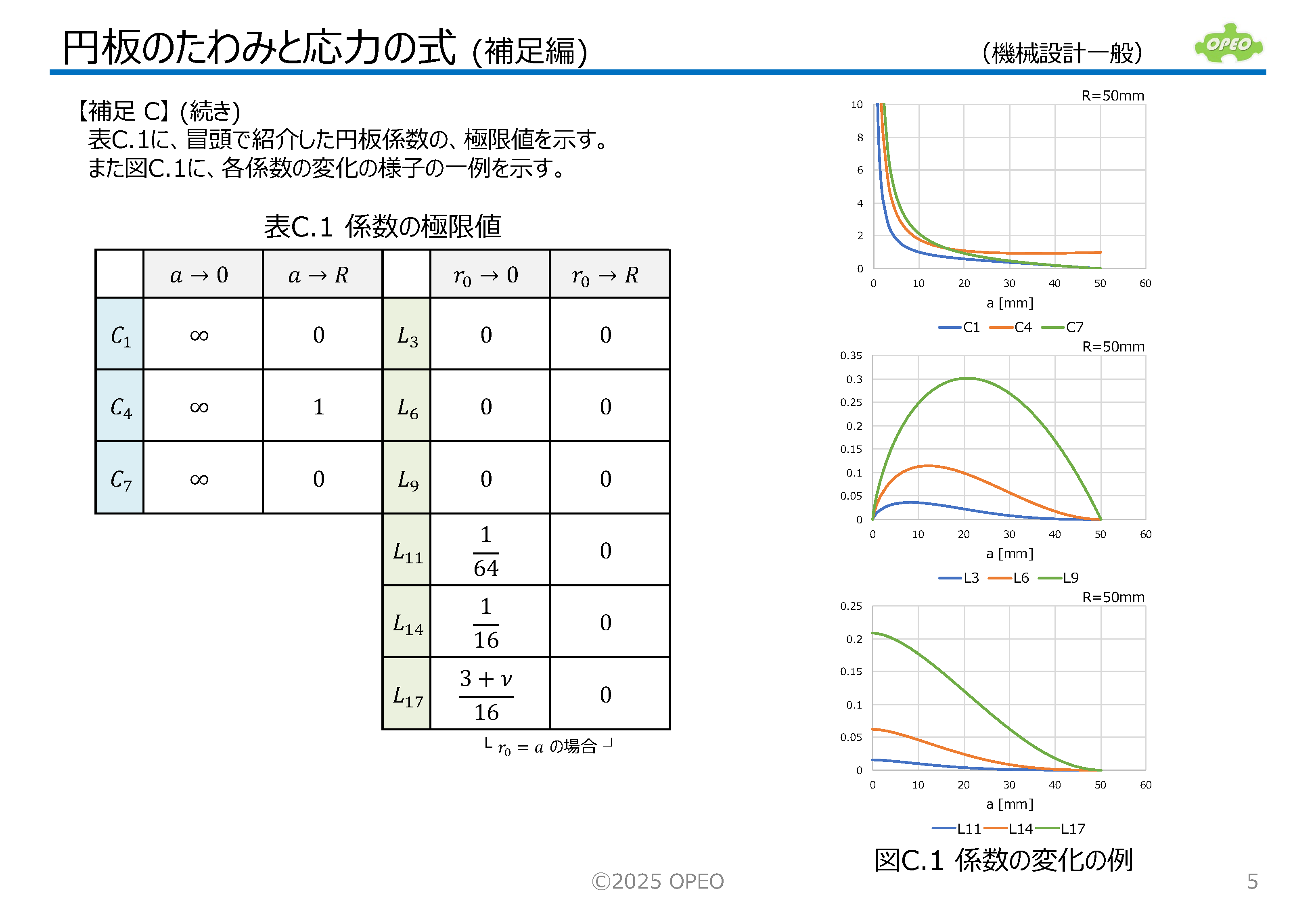
掲載記事で紹介した式に基づいて、集中荷重と等分布荷重の計14種類のケース別に、たわみと応力を計算するExcelシートです。
領域サイズや半径位置により、たわみや応力がどのように変化するかを、グラフィカルにイメージできるよう、簡単なグラフも表示します。
<更新履歴>
・revB：材質と材料をプルダウンメニューから選択すると、対応した物性値をセットするようにしました。
（材料データシートはカスタマイズ可能)
・revC：円板の侍従を考慮した計算に対応しました。
・revD：計算用データ列の表示/非表示ボタンを追加しました。
3Dグラフ(等高線グラフ)を追加し、たわみと応力の状態を立体的に確認できるようにしました。
ケースNo.のプルダウンから、境界条件のケース番号を選択すると、対応したグラフに更新されます。
本バージョンから、動作対象の環境はExcel2021および365以降となります。
2025.11.19 更新 (revC1→revD)
