2点支持はりとベッセル点
15,022
|
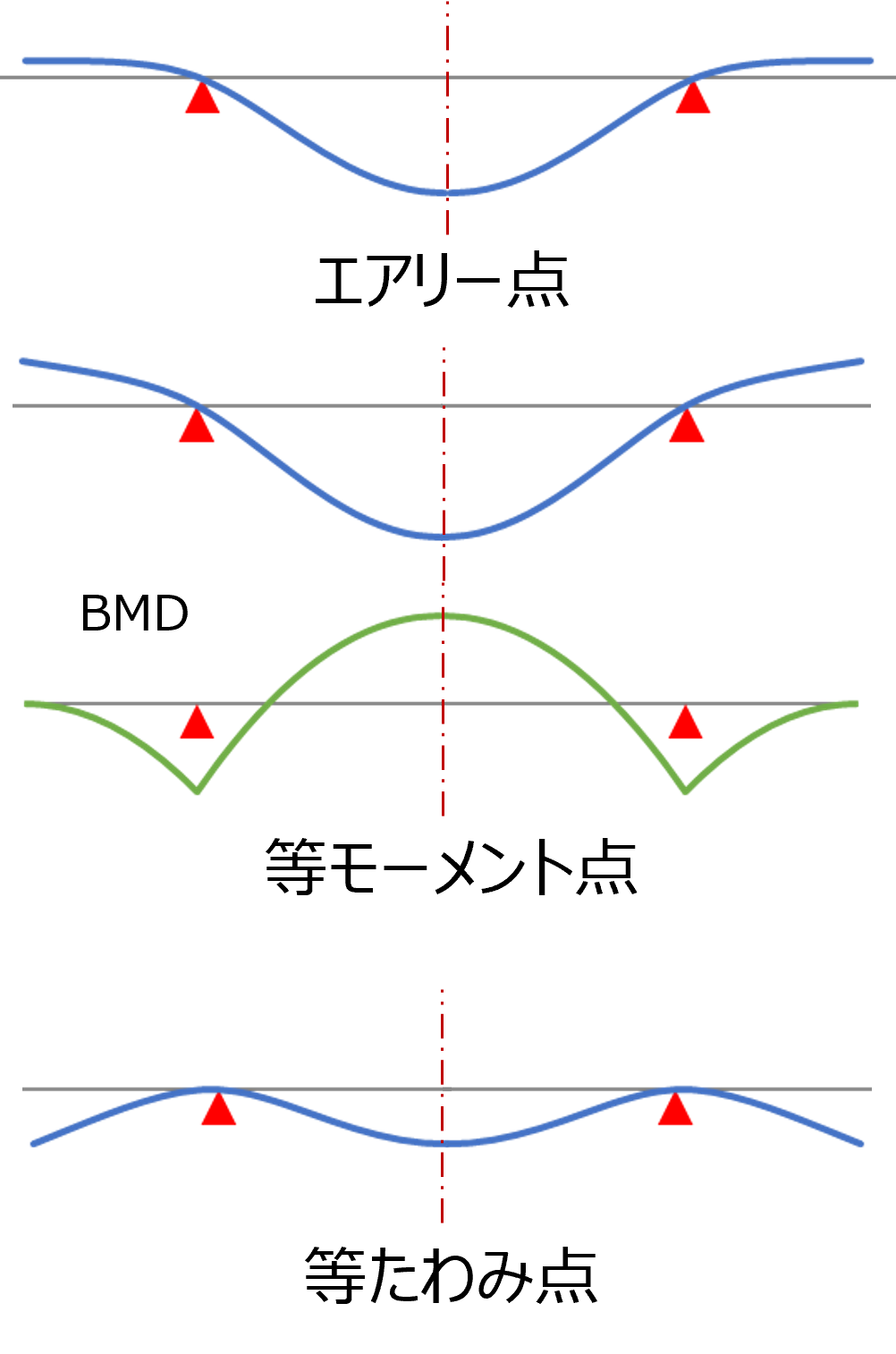
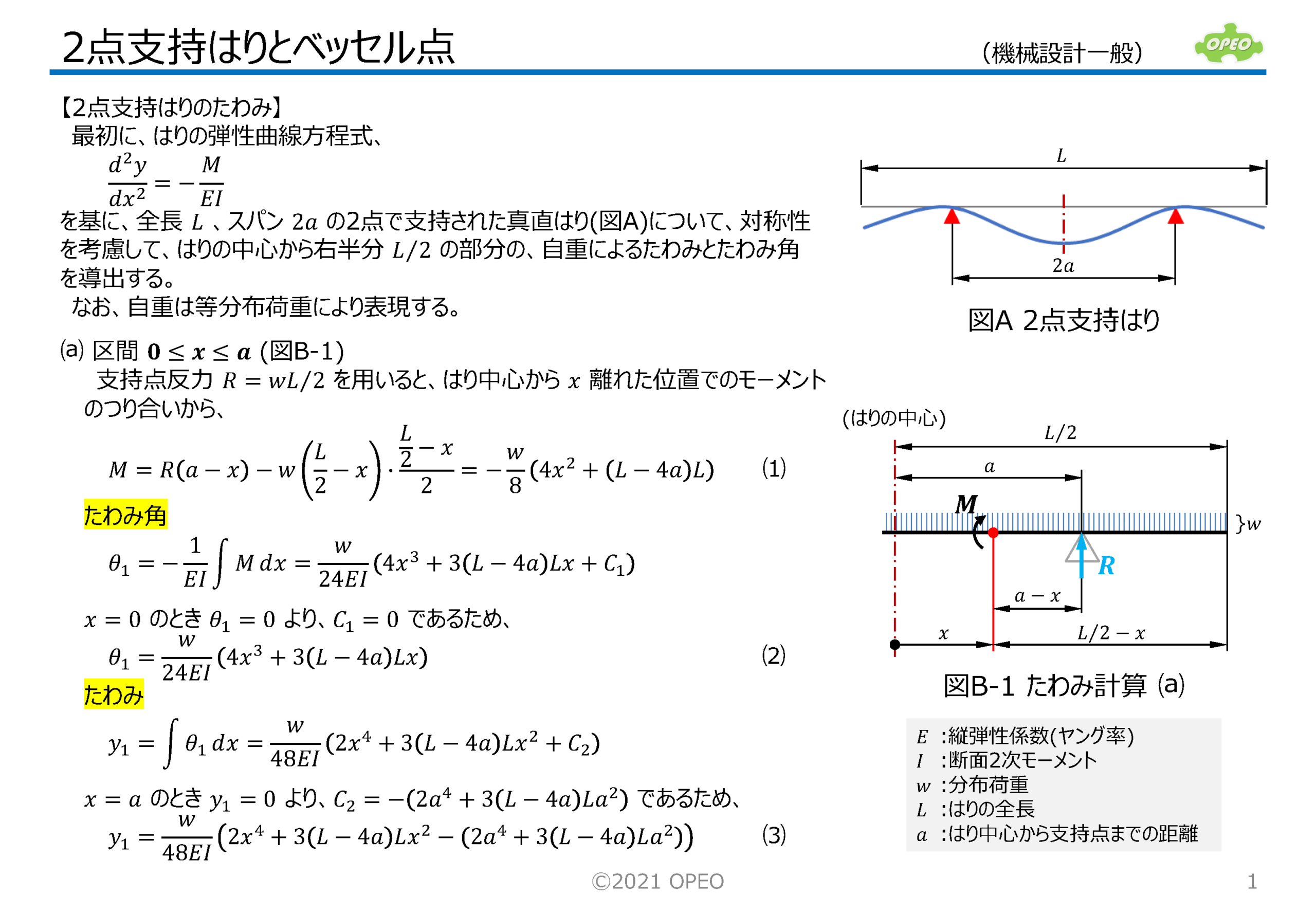
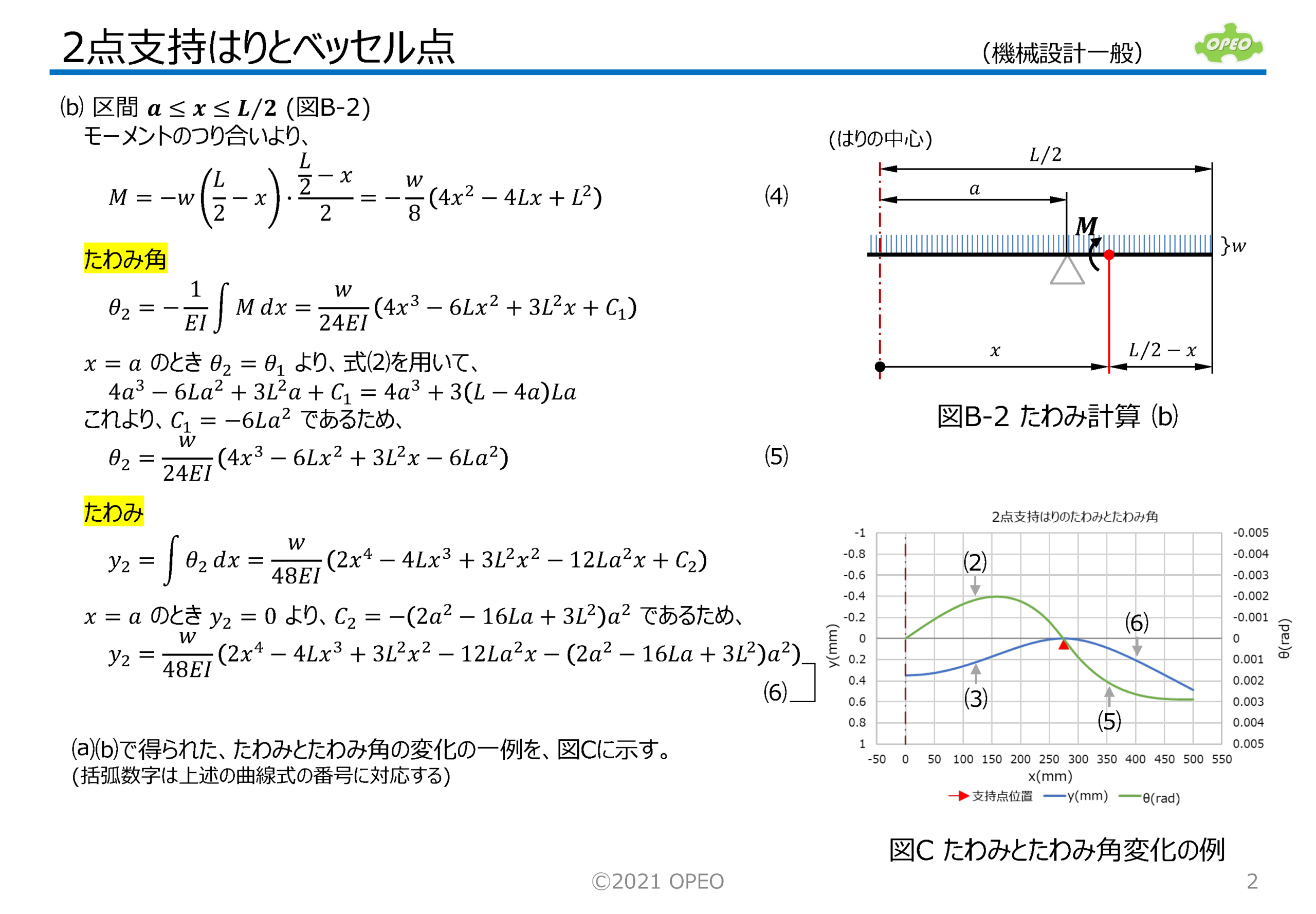
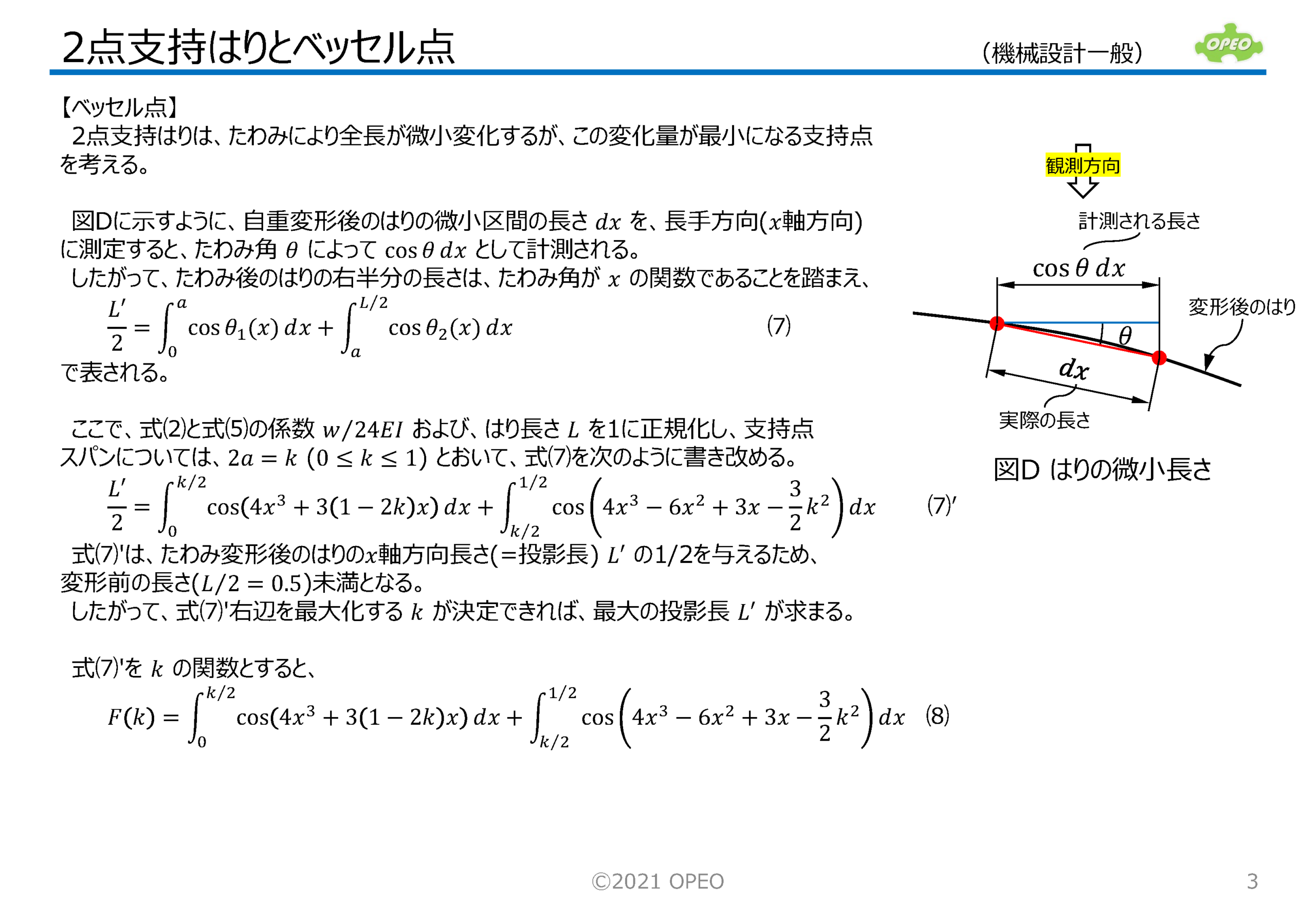
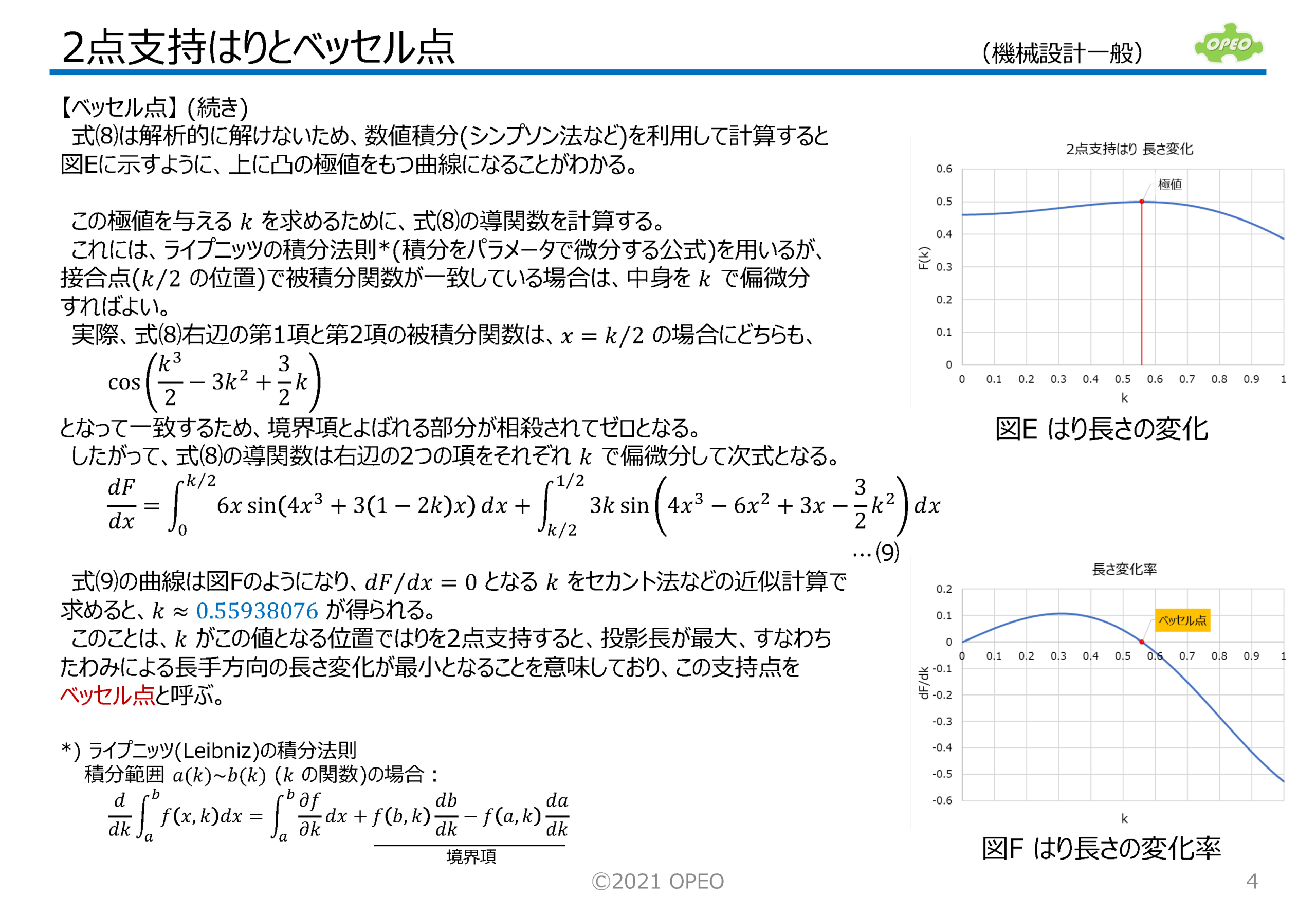
真直はりを、中心から対称位置にある2点で支持した場合、たわみにより全長が微小に変化しますが、この変化量が最小になる支持点をベッセル点と呼びます。 ここでは最初に、弾性曲線方程式を使って2点支持はりのたわみの式を導出し、次にベッセル点算出の考え方を解説しています。 ペッセル点の値の算出には、やや複雑な三角関数の積分が必要で、一般には多項式近似による計算で求める方法が紹介されていますが、本項では数値積分を用いて計算した結果を示しています(ただし、実用上の差はありません)。 2点支持はりのその他の特殊支持点である、エアリー点、等モーメント点、等たわみ点の位置についても、簡単に式の導出方法を説明しています。 大まかに言って、支持点が0.55から0.59の範囲にあれば、はりはそれなりの姿勢で安定している、と理解していただければいいと思います。 なお、ここで解説した計算方法を使ったExcelシートも公開しています。 |
 |
<参考規格>
・JIS B7506:2004 ブロックゲージ
<参考URL>
https://ja.wikipedia.org/wiki/ベッセル点
https://ja.wikipedia.org/wiki/弾性曲線方程式
https://ja.wikipedia.org/wiki/三次方程式#ビエトの解
3次方程式の解の公式-婆茶留高校数学科

2点支持はりとベッセル点Excel
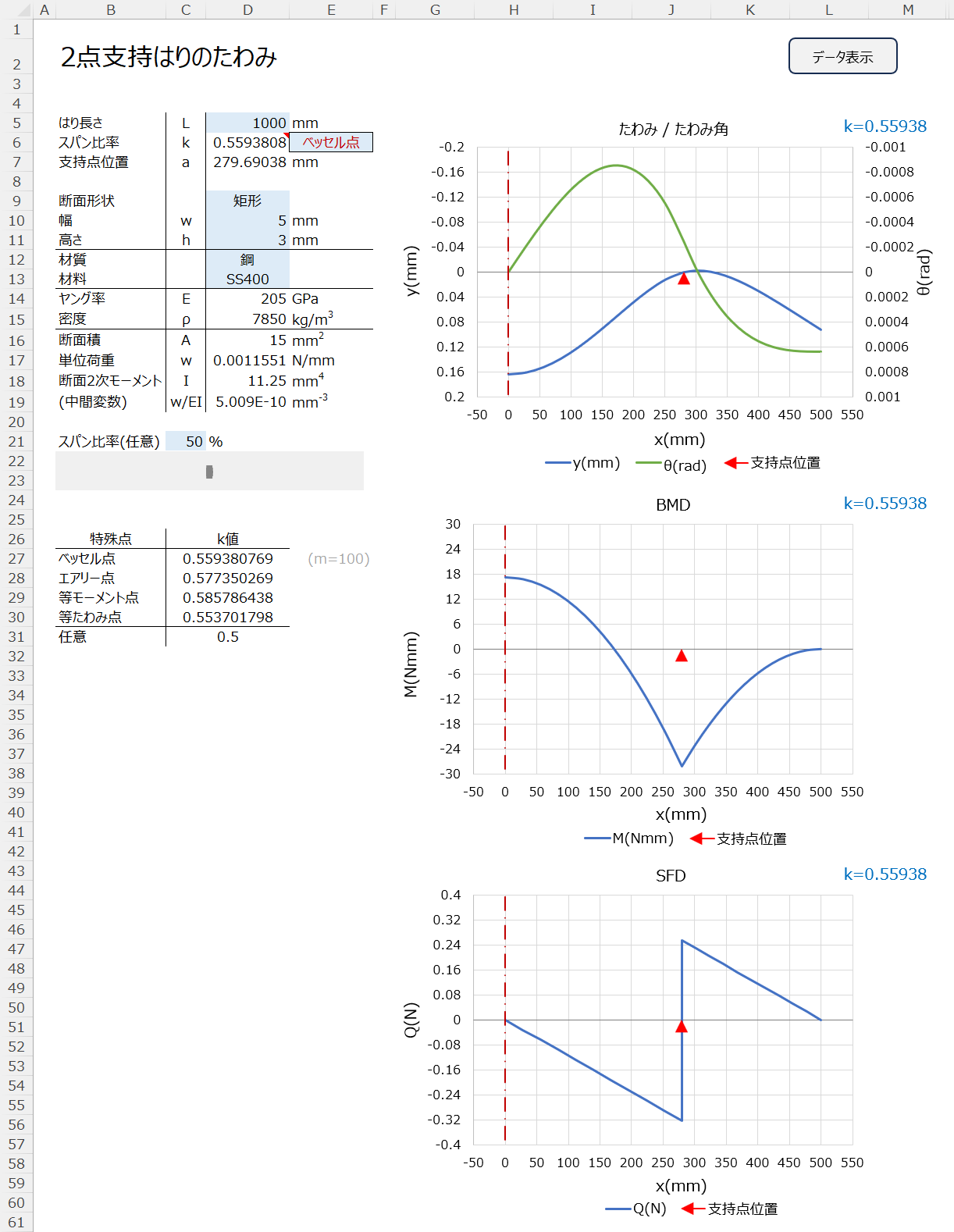
このExcelでは、2点支持はりのたわみ、たわみ角、SFD、BMDについてグラフ表示します。
なお、これにはベッセル点を求めるための数値積分及び近似計算コードを記述したVBAを含みます。
また、エアリー点、等モーメント点(中央と支持点の曲げモーメントが等しい)、等たわみ点(中央と端部のたわみが等しい)も表示します。
特にロックはかけていないので、興味のある方は参考にして下さい。
<更新履歴>
・revH1:本バージョンから、動作対象の環境はExcel2021または365以降となります。
・revH2:UIを一部改良しました。
・revI:ベッセル点の計算方法を改良しました。
2026.2.23 更新 (revH2→revI)
DL解除コード:a508
