慣性モーメントと重ね合わせの原理

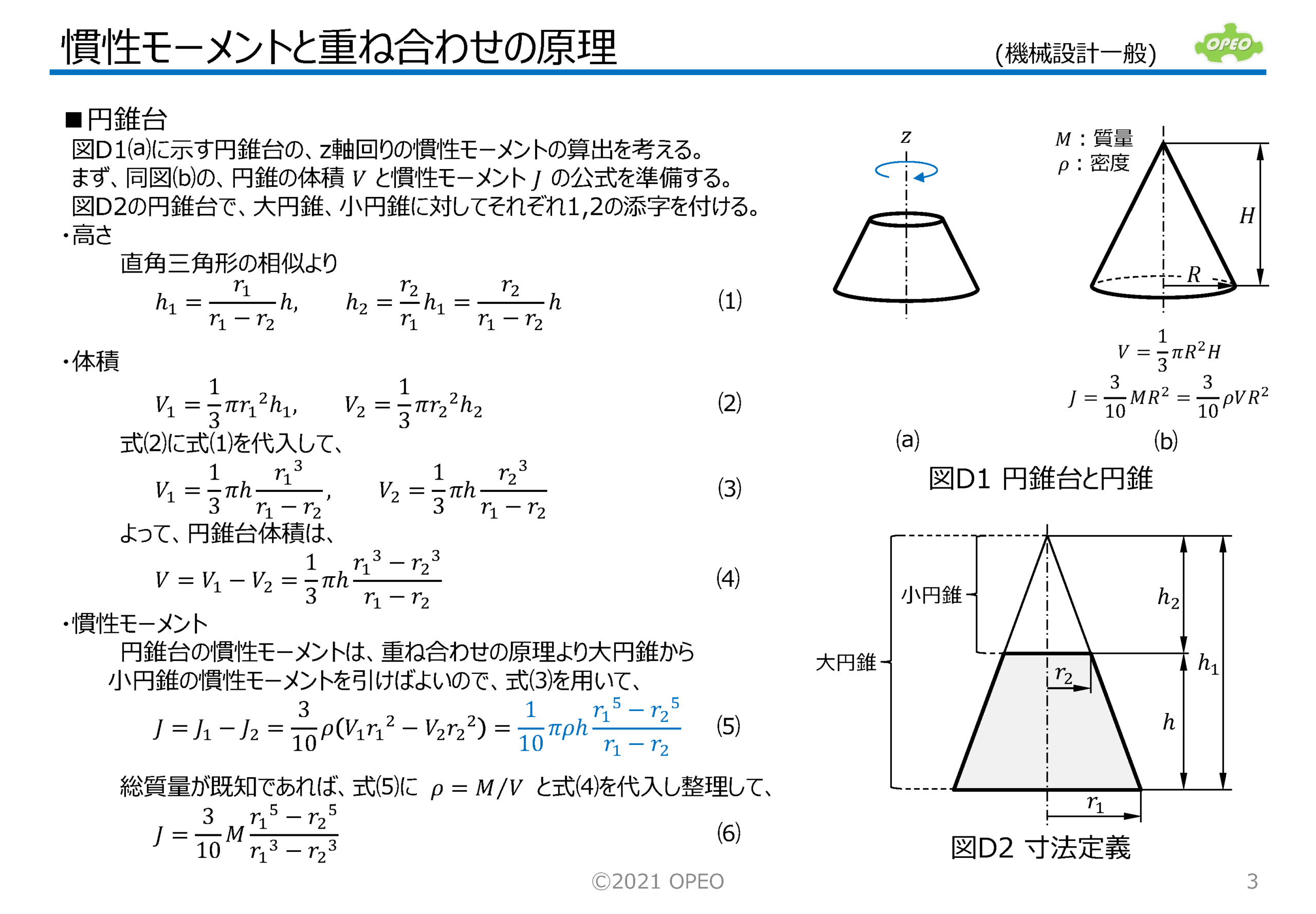
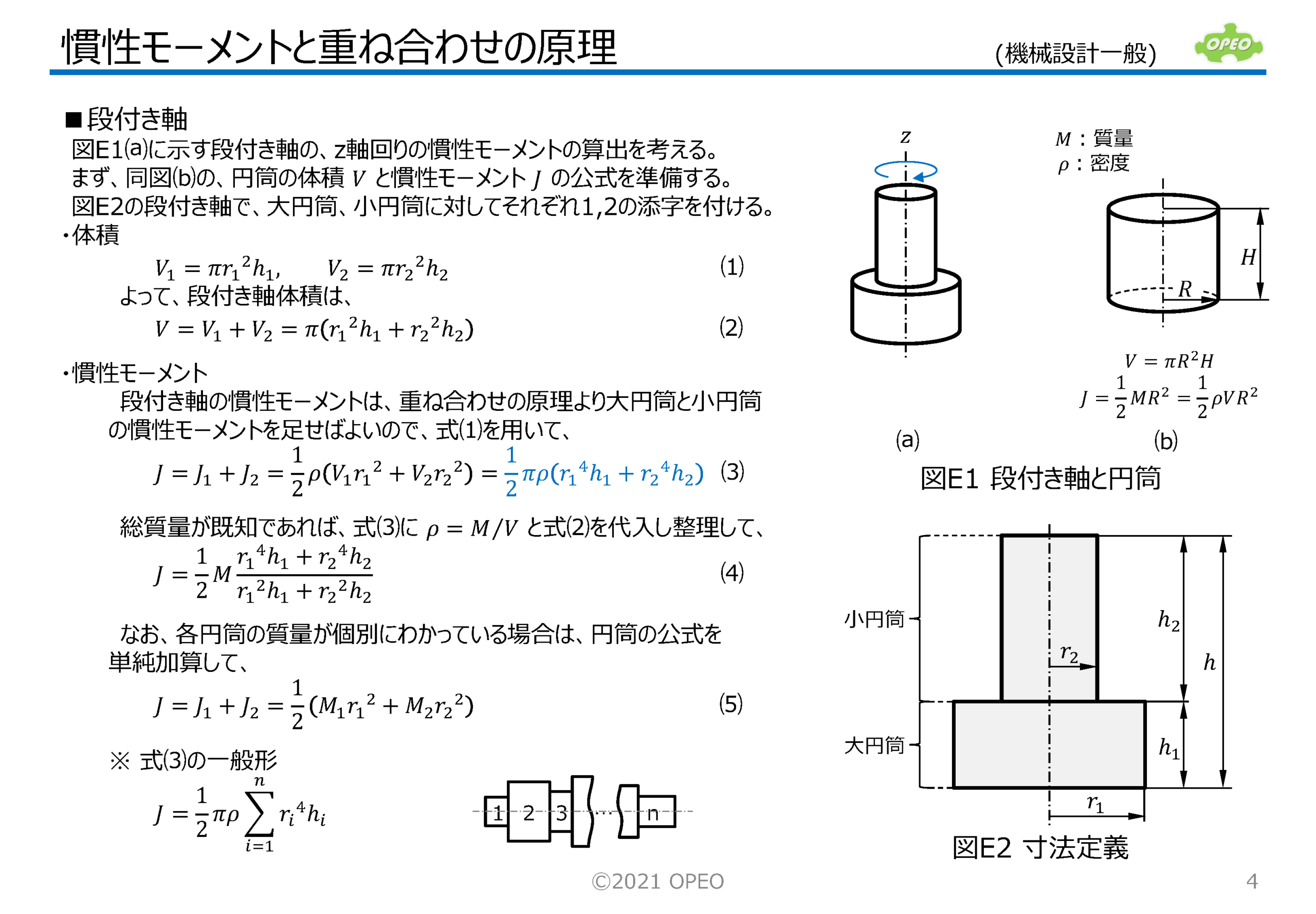
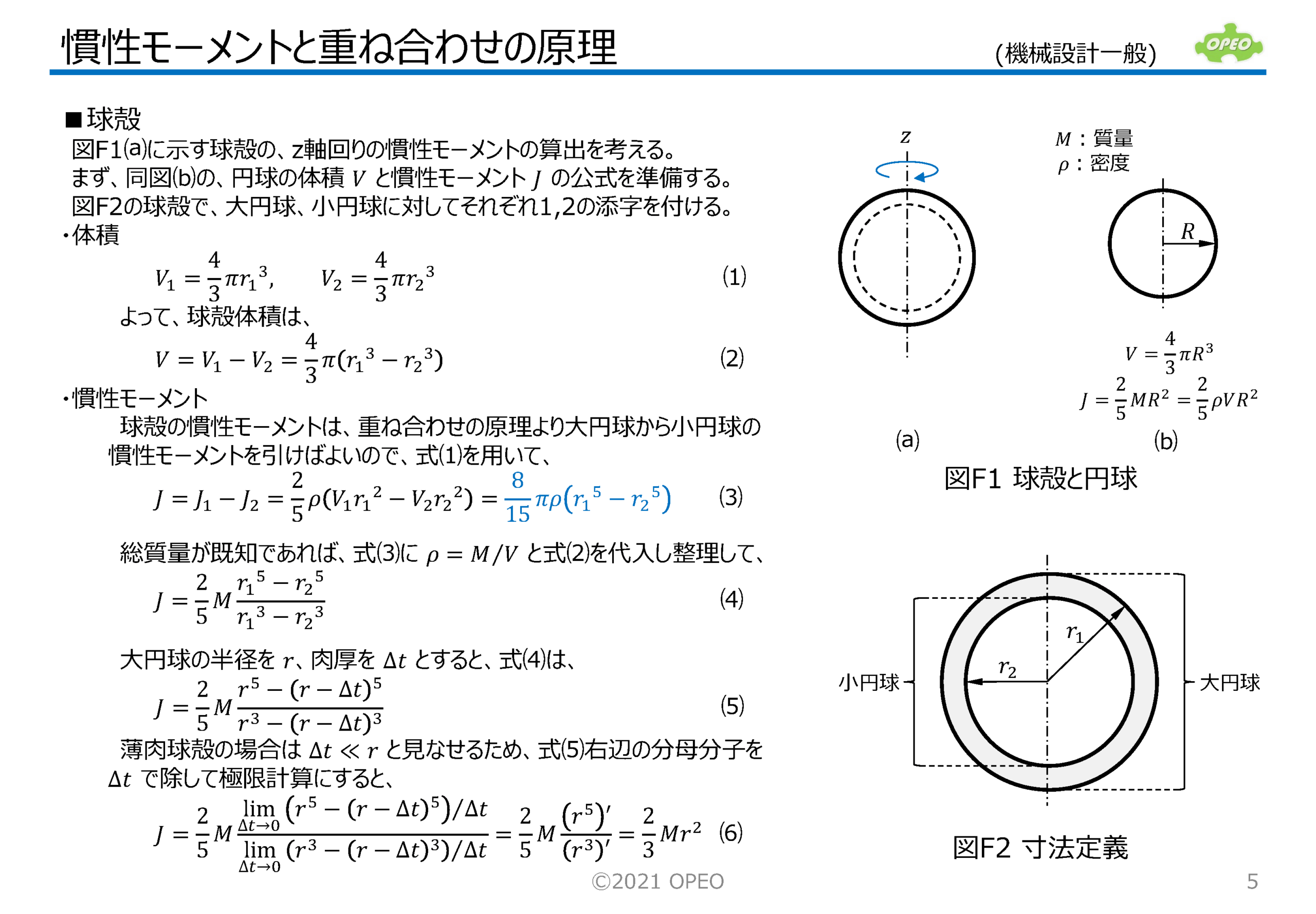
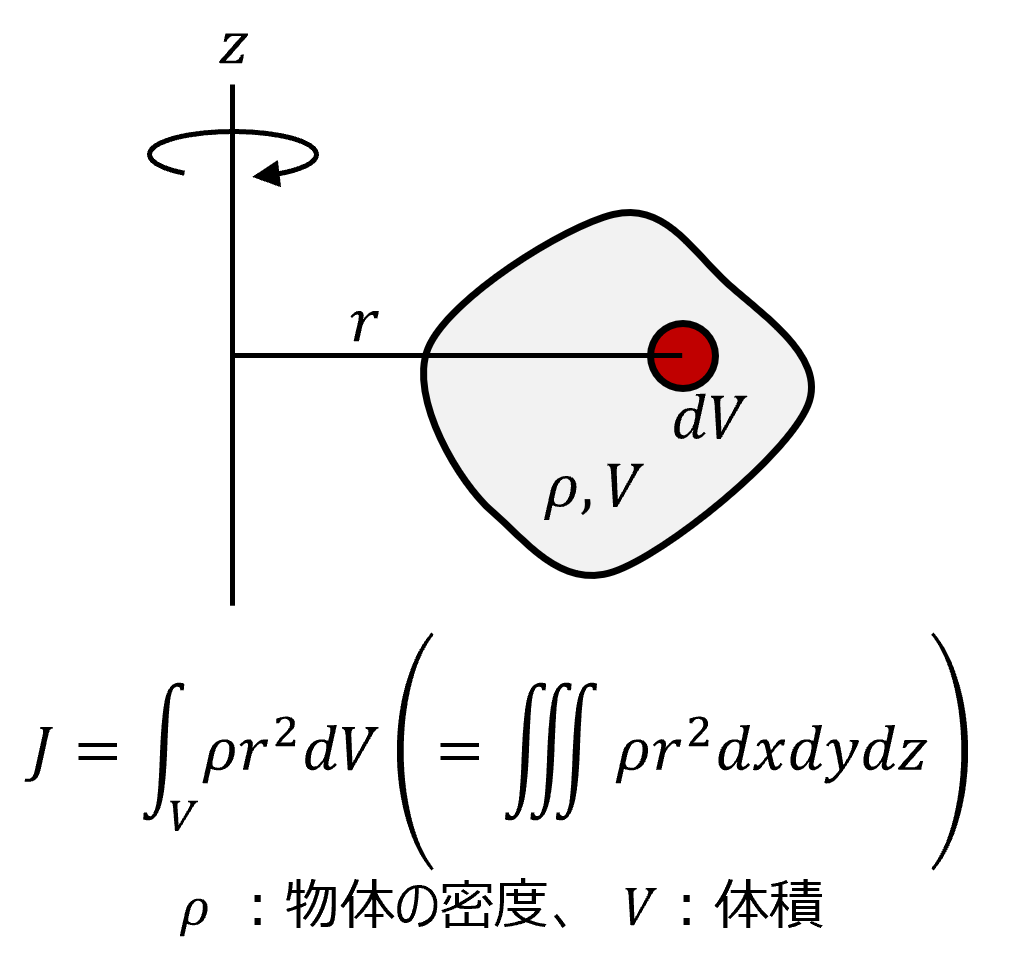
　動力学で扱われる「慣性」は、物体が動き続けようとする、もしくは動きの変化に抵抗する量です(慣性の法則)。
　回転体では、物体が回り続けようとする、もしくは回転の変化に抵抗する量となり、これを「慣性モーメント」と呼びます。
　回転体の慣性モーメントは、理論的には体積積分(三重積分)で定義されますが、直方体や球、円筒などの基本形状については公式があります。

　また実用的な物体形状は、多くの場合これら基本形状に分解できるので、慣性モーメントの計算はそれら既知の公式を組み合せれば積分計算をすることなく行えます。
　その前提となっているのは、 “重ね合わせの原理” という重要な原理です。

　ここでは、この重ね合わせの原理を利用した慣性モーメントの計算方法を、いくつかの例を交えて解説します。
　(なお、慣性モーメントの記号は通常 I が使われますが、断面2次モーメントと明確に区別するため、ここでは J に統一しています)

　この記事に関連した動画をYouTubeで公開していますので、参考にしてみて下さい。