歯形係数
16,191
|
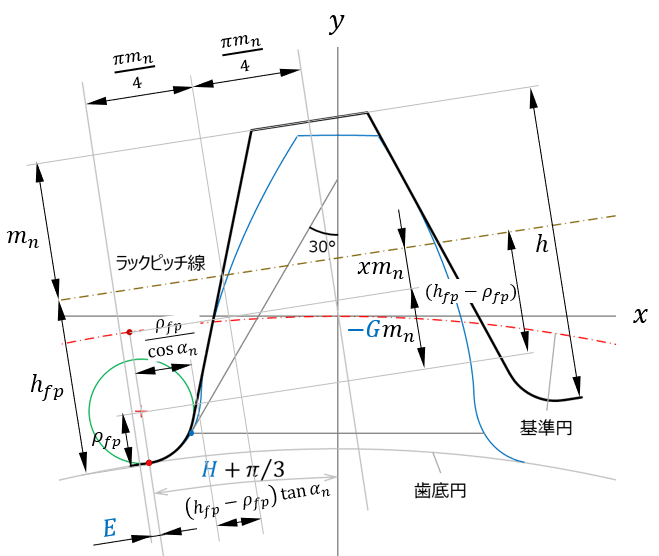
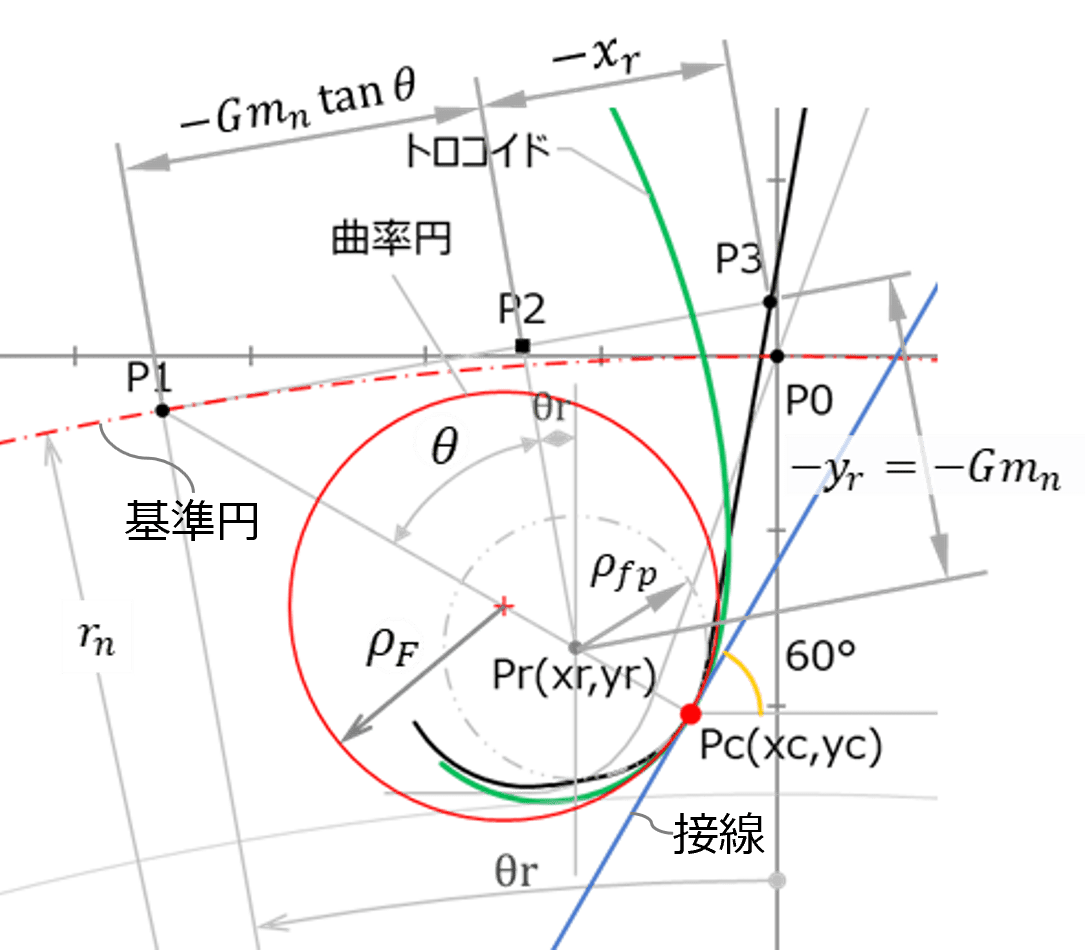
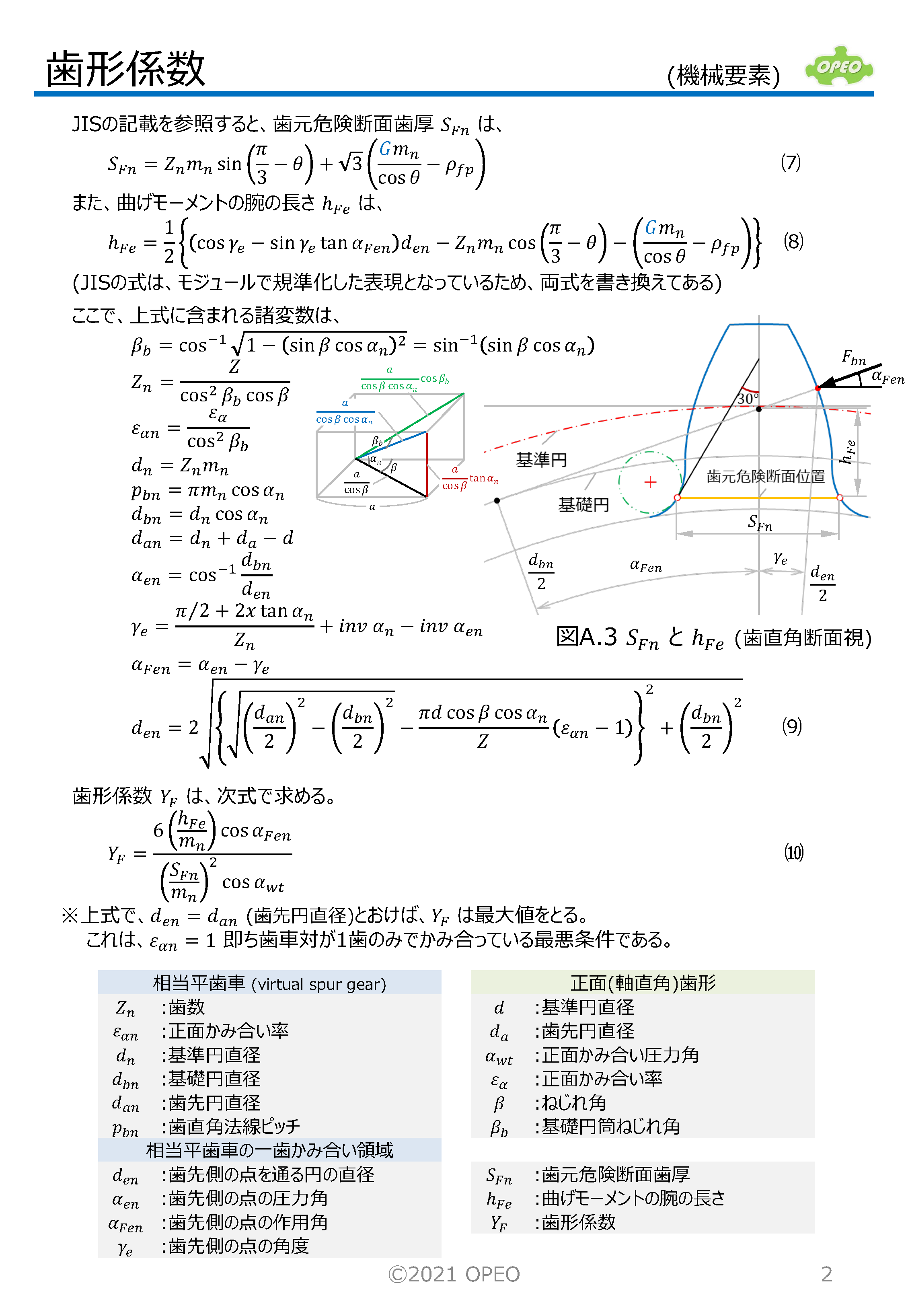
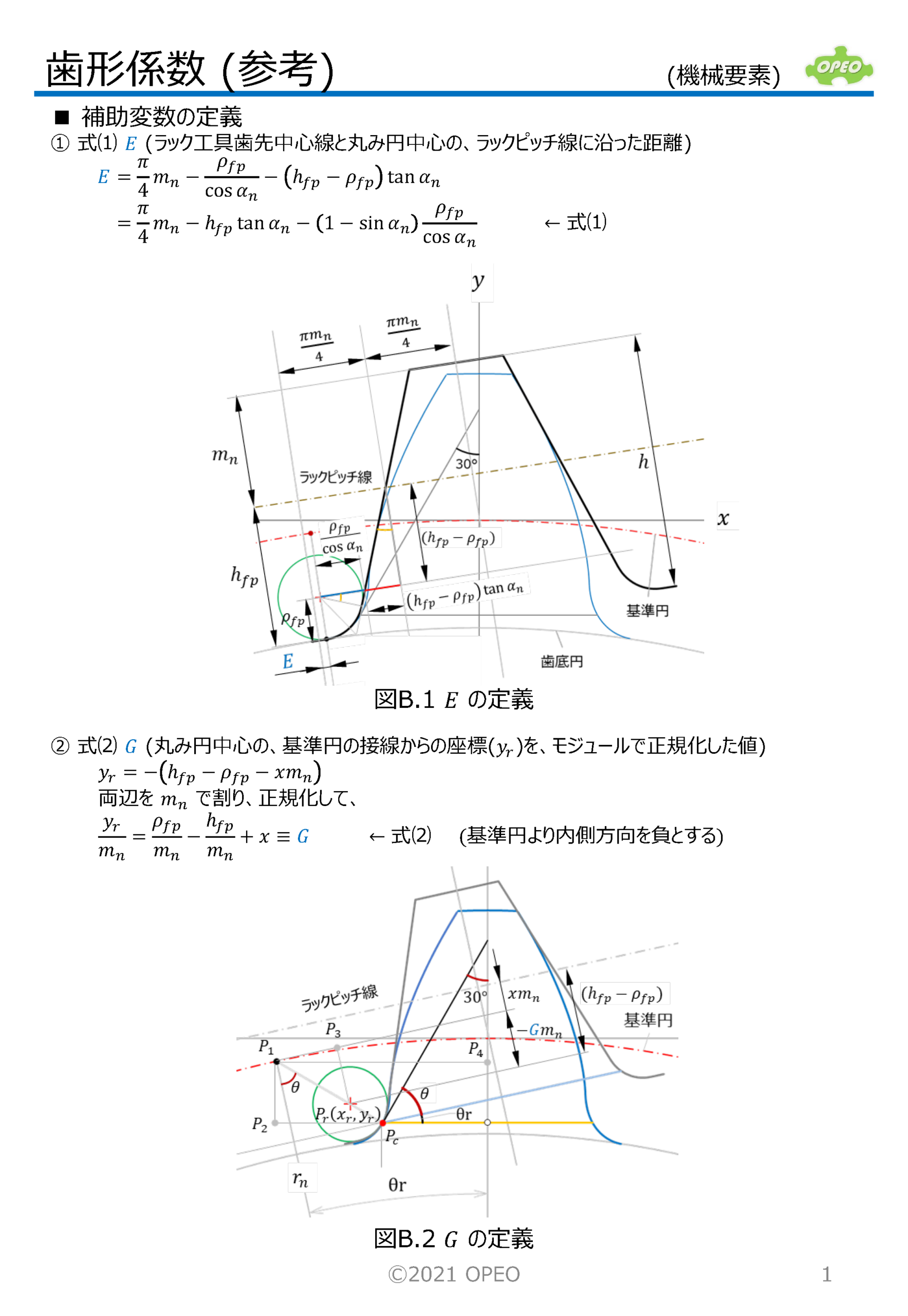
歯車の強度計算では、前もって歯形係数を求めておく必要があります。 なおJISの式では、記事中のθを求めるために補助変数を定義して計算していますが、30°接線位置までのラック工具回転角θrが求まれば、これらの変数を用いる必要はありません(JIS式は、ラック工具刃先が歯底円と接している状態から、30°接線との接点位置まで回転する角度を計算しています)。 このθrは、別掲記事(歯形曲線の接線)内の計算方法により求めることが可能です(θrが求まれば接点座標も求まります)。
|
|
|
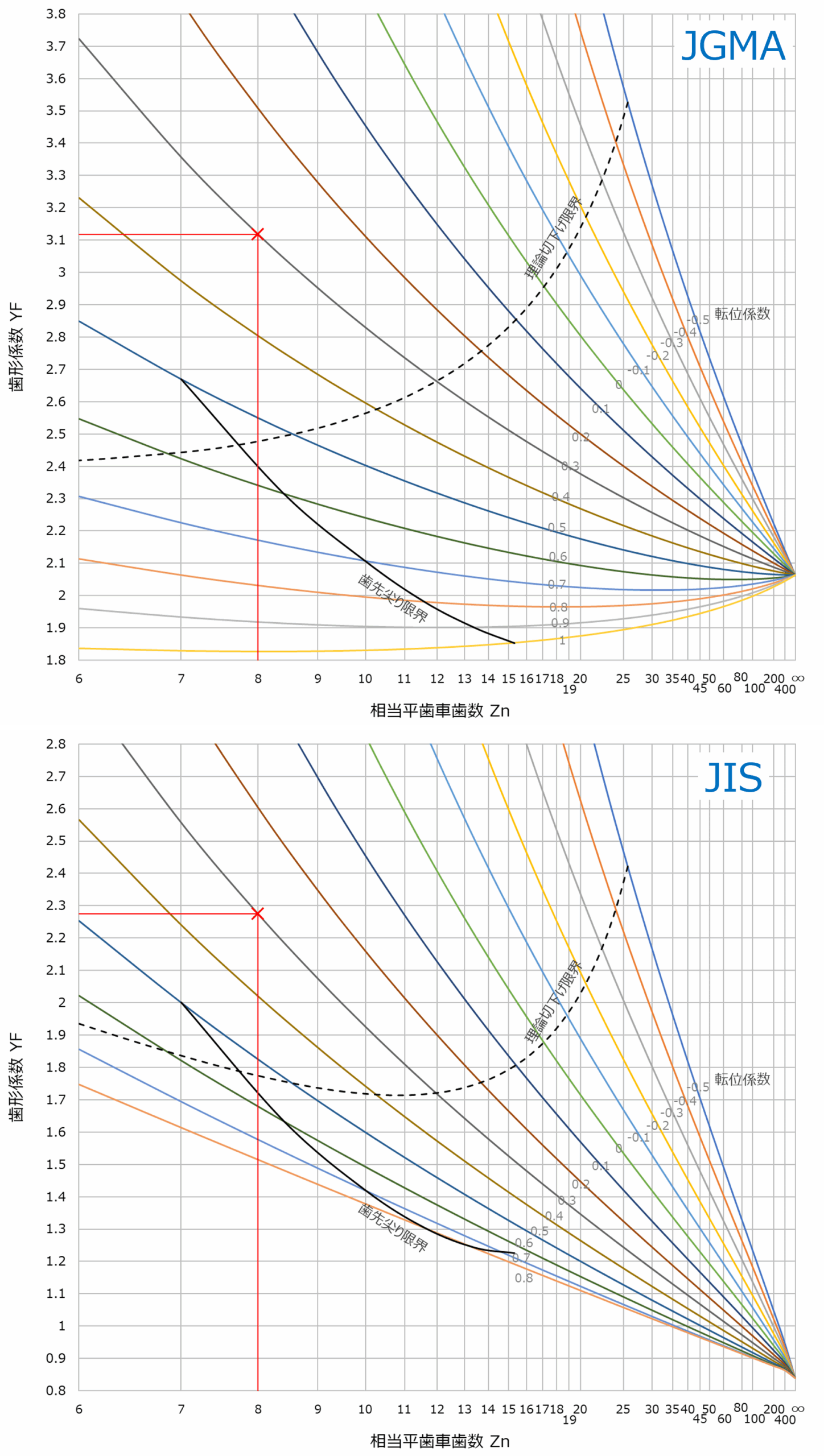
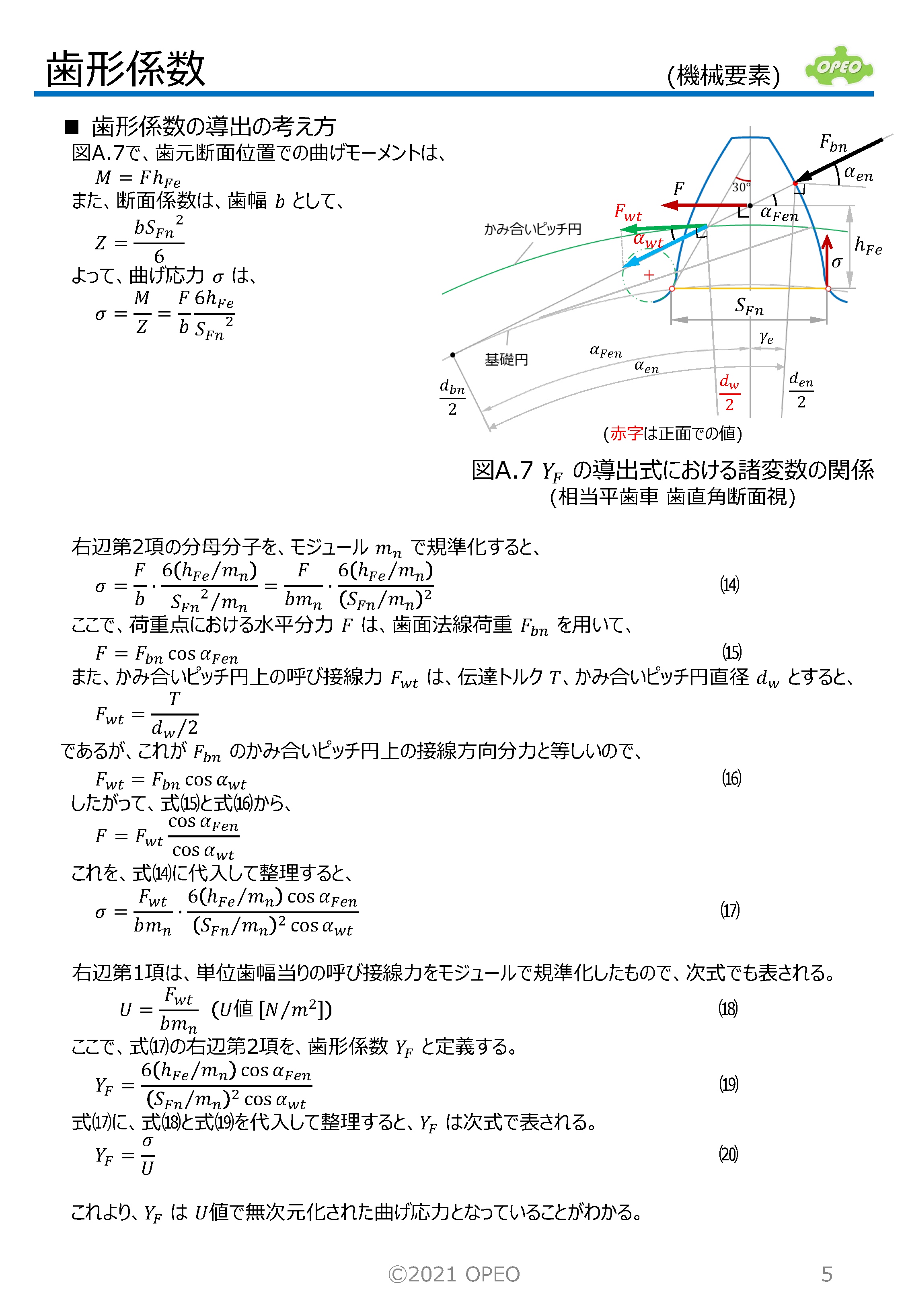
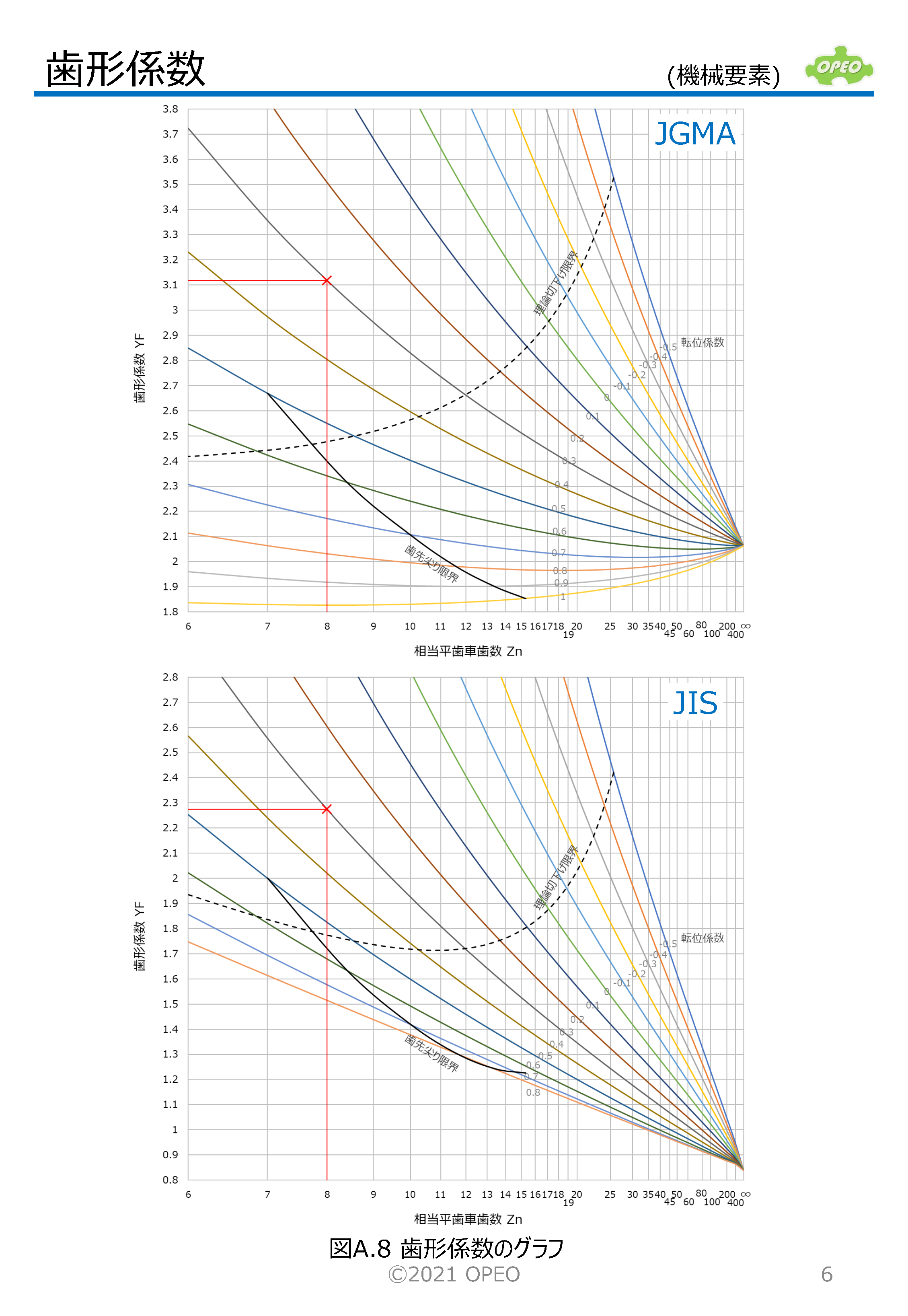
ちなみに、歯形係数の式にはモジュール(mn)の項が入っていますが、最終的にはこれは相殺されて、歯形係数自体はモジュールの大きさには無関係となります。 本記事の内容を元に作成した、歯形係数計算Excelシートも参考に添付しています。 |
JGMA式
JIS式
|
<参考規格>
・JIS B1759:2019 プラスチック円筒歯車の曲げ強さ評価方法
・ISO 6336-3:2019 Calculation of load capacity of spur and helical gears – Part3:Calculation of tooth bending strength
<参考資料>
・小原歯車工業㈱ 歯車技術資料
・塚本,金丸 (1971), “平歯車の曲げ強度計算式における歯形係数”, 機械設計 第15巻第8号, 日刊工業新聞社
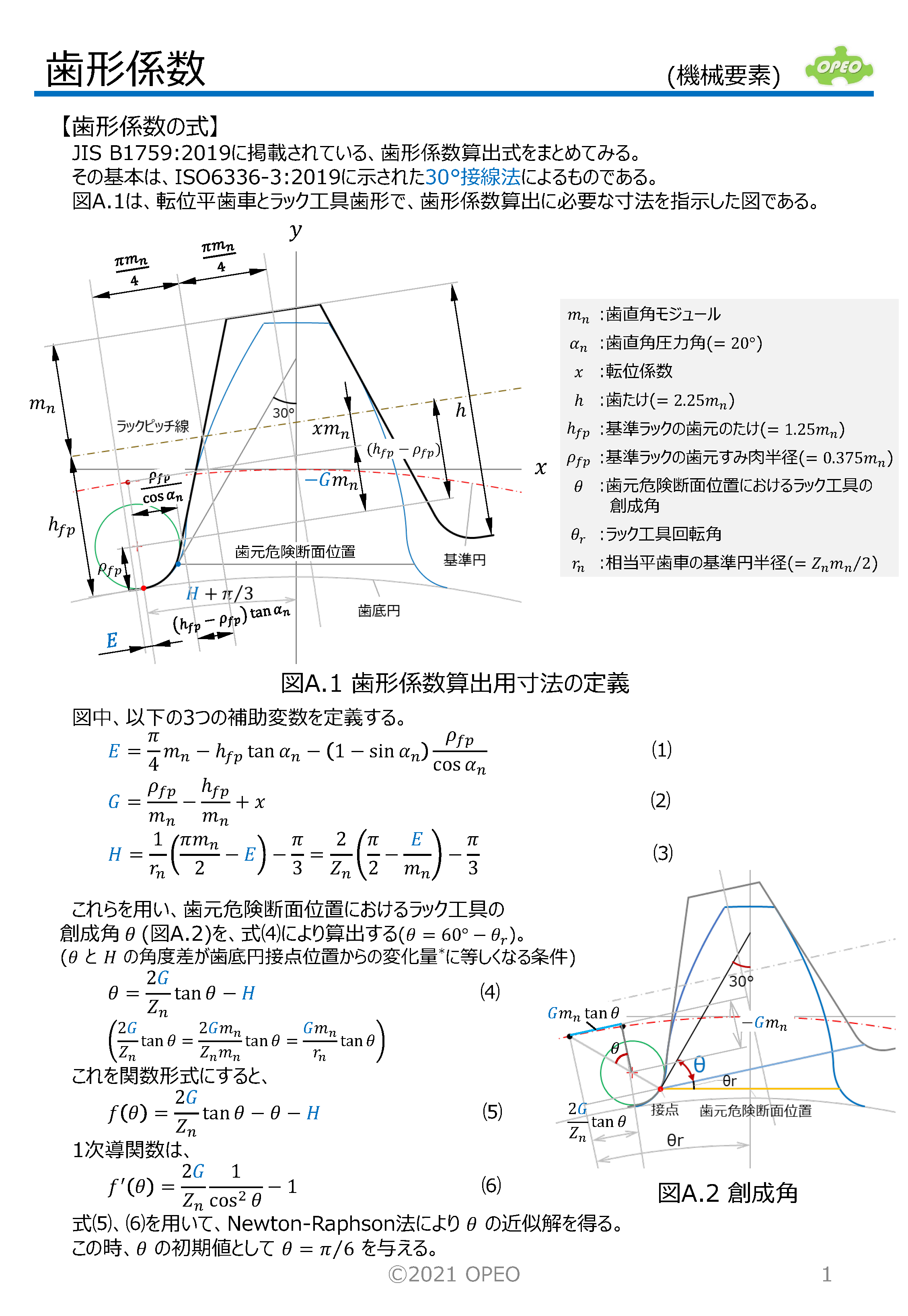
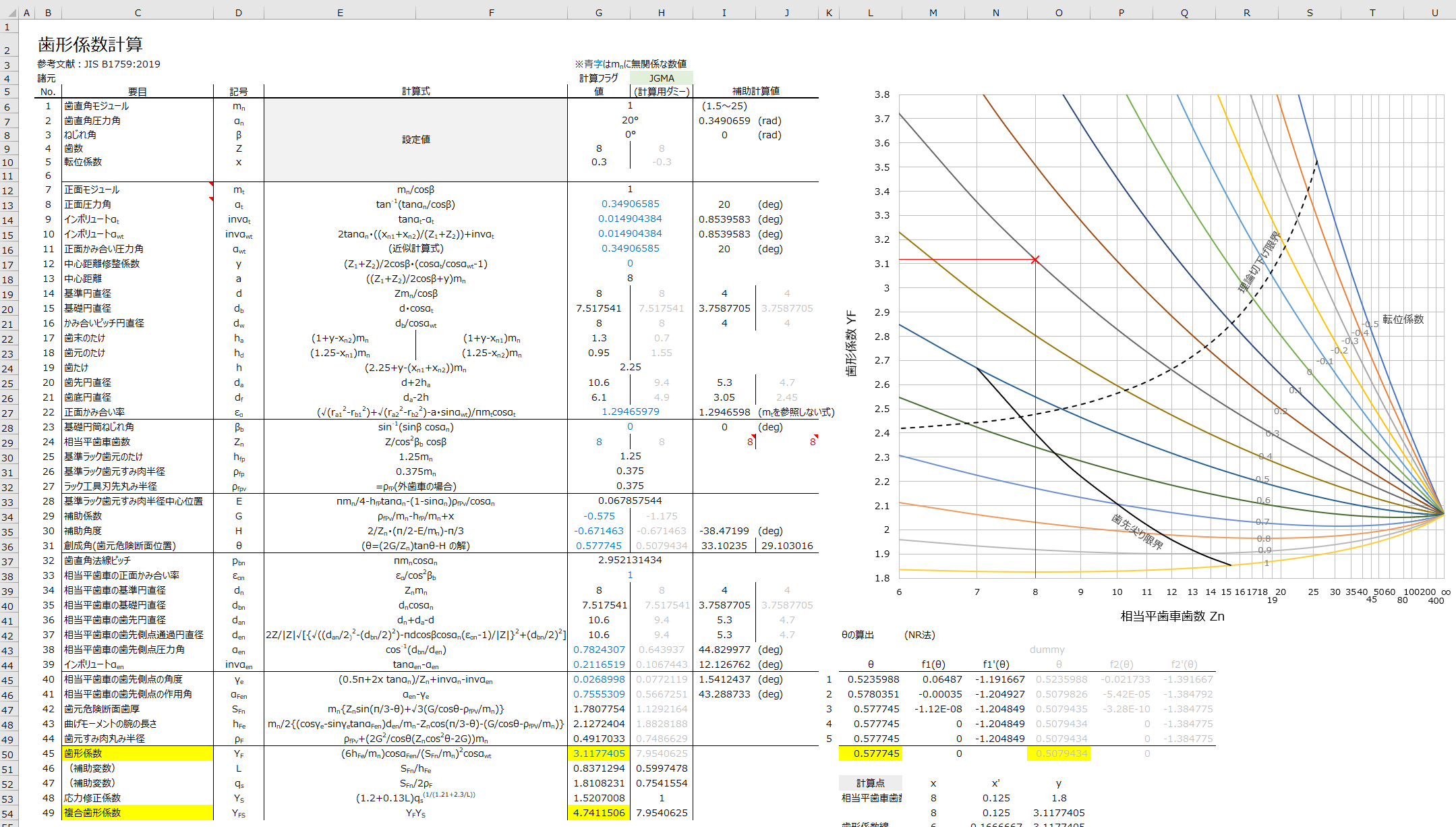
歯形係数計算Excel
本稿の計算式に基づいて歯形係数を計算するExcelシートです。
計算結果の確認用に、計算点をグラフ上に表示します。
なお、このグラフは、歯数6以上の歯形係数に対応しています(revH以降)。
注意： revIまでは、計算式記述ミスによりねじれ角が0°以外の場合に歯形係数が正しく計算されていません。
この不具合はrevJ以降で修正してあります。
マクロにはロックをかけていますが、中身を確認したい方はお問合せフォームよりご依頼いただければ、ロック解除版の提供も可能です。
2023.6.10 更新 (revI→revJ)
