スプライン曲線

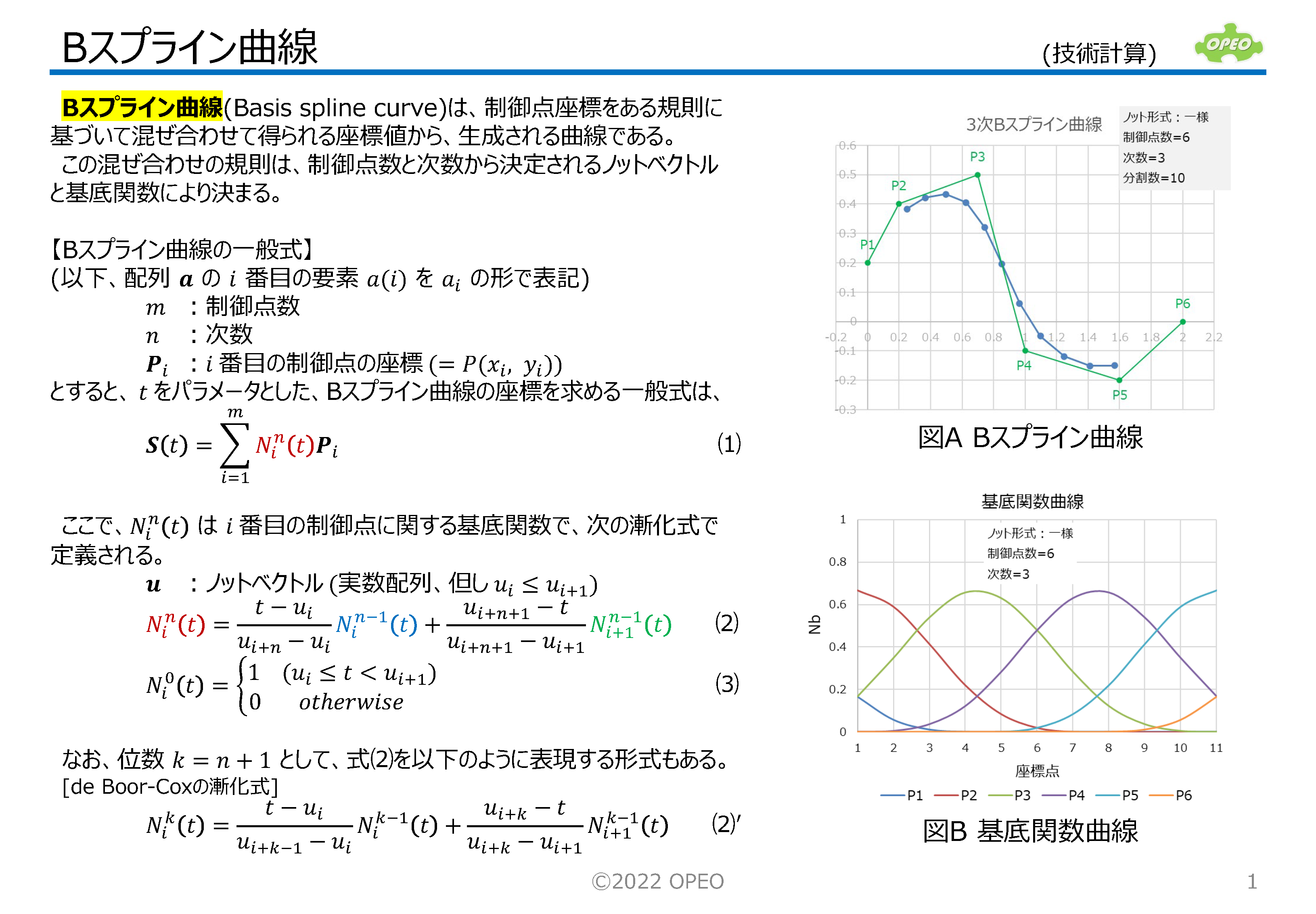
　曲線をn次多項式で近似する手法の、いくつかについて解説します。
　これらは、CAD上で曲線や曲面を表現する上での、基本的な手法となります。

　例えば、右図のような6つの点からなる経路（パス）を考えます。

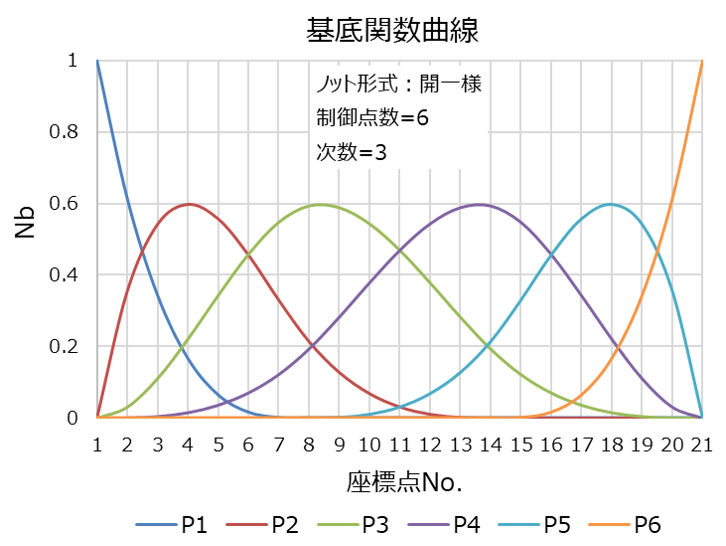
　この経路に沿って滑らかに描かれる曲線には、下図のようなものがあります。
　①は全ての点を通過点として通るスプライン曲線（3次）、②③は全ての点を制御点として作られる各々ベジエ曲線（5次）、Bスプライン曲線（3次）となります。

　ちなみに、③の3次Bスプライン曲線の次数を5次に上げる、即ち次数を[制御点数-1]とすると②の5次ベジエ曲線になります。つまりベジエ曲線は、Bスプライン曲線に次数制限をかけた特別な曲線です。

　なお、①の3次スプライン曲線には、各区間（P1～P2、P2～P3、…）毎に通過点での連続性を考慮した3次関数曲線が適用されています。

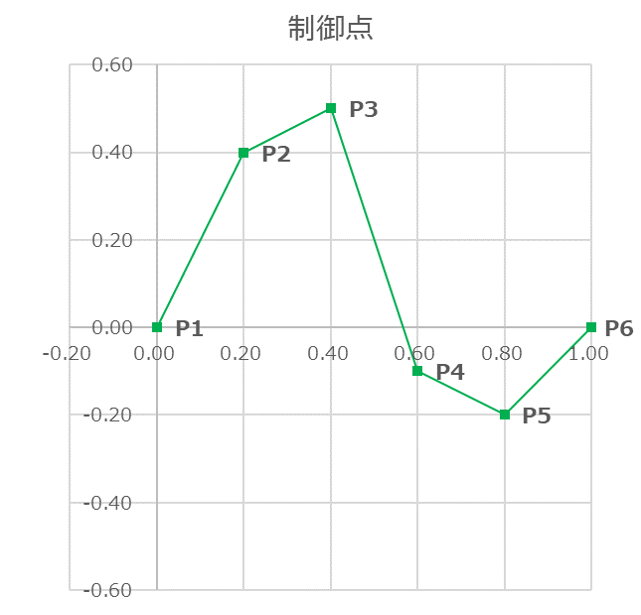
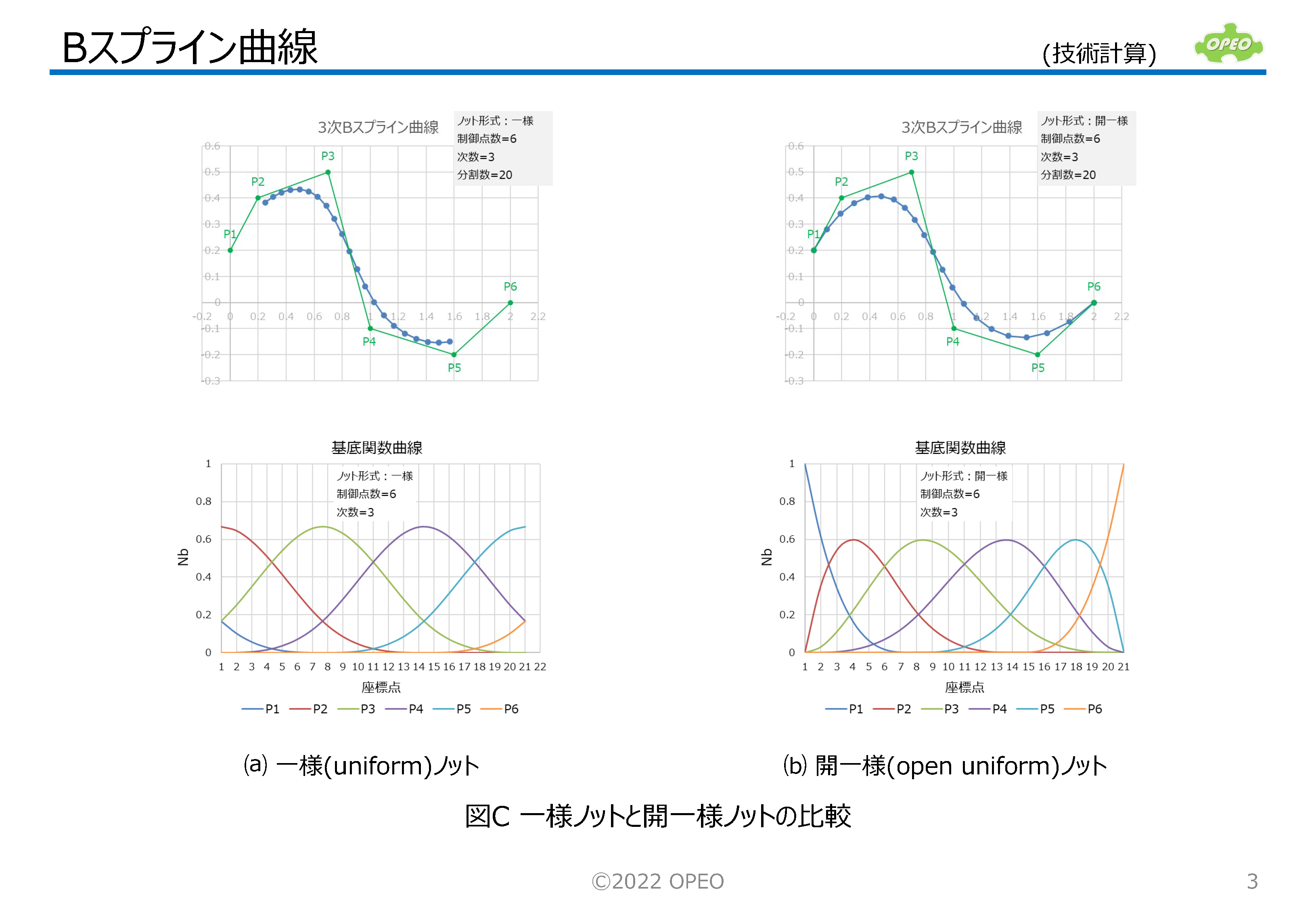
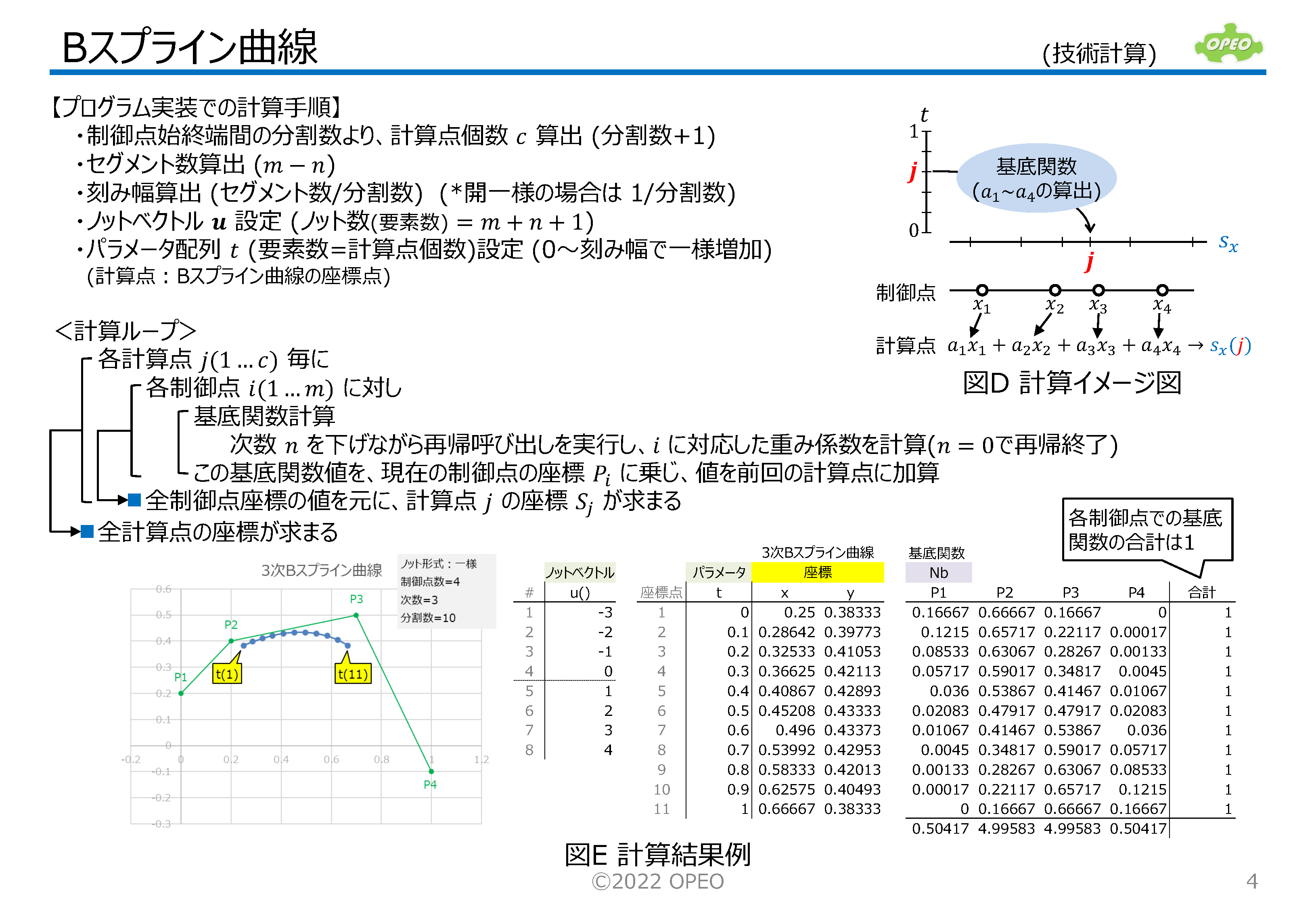
　Bスプライン曲線は、基底関数によって、各制御点の座標値の寄与度(重み)を計算座標に振り分けることにより生成されます。

　右のグラフは、上図③の制御点数6、次数3のBスプライン曲線の計算座標点(1～21番)に対する、基底関数の値の変化を示したものです(なおこのグラフは、”開一様ノットベクトル”という、始終点が制御点と一致するBスプラインについて計算したものです)。

　このグラフから、並び順が中央に近いP3やP4の制御点の座標値は、Bスプライン曲線の両端点を除いた、全域の曲線座標計算に使われていますが、その他の制御点座標値は、ほぼその点の近くの曲線座標計算にのみ使われていることがわかります。
　なお、同一座標点における基底関数値の和は常に1となる、ことに注意して下さい。