2次曲面の一般式
577
|
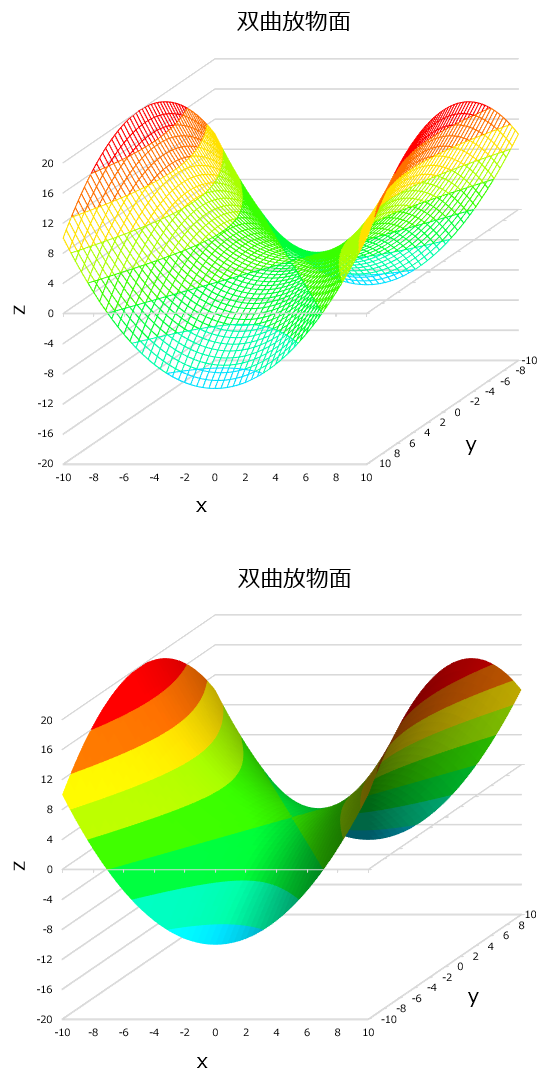
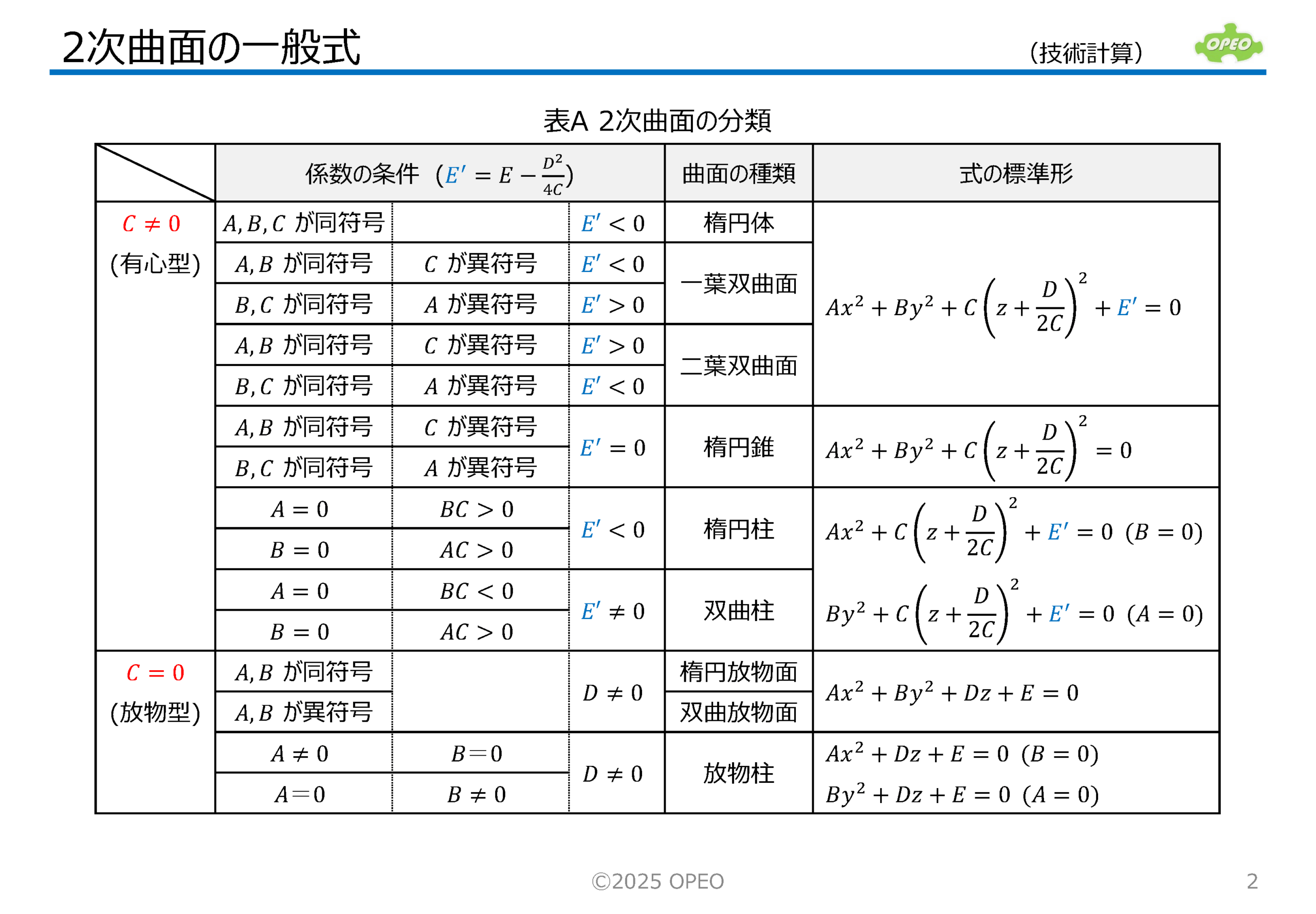
2次曲面の一般式をまとめた記事です。 基本式は、
本記事では、これらの式で表される曲面について、係数の条件を表形式にまとめてあります。 |
 |

2次曲面サンプルExcel
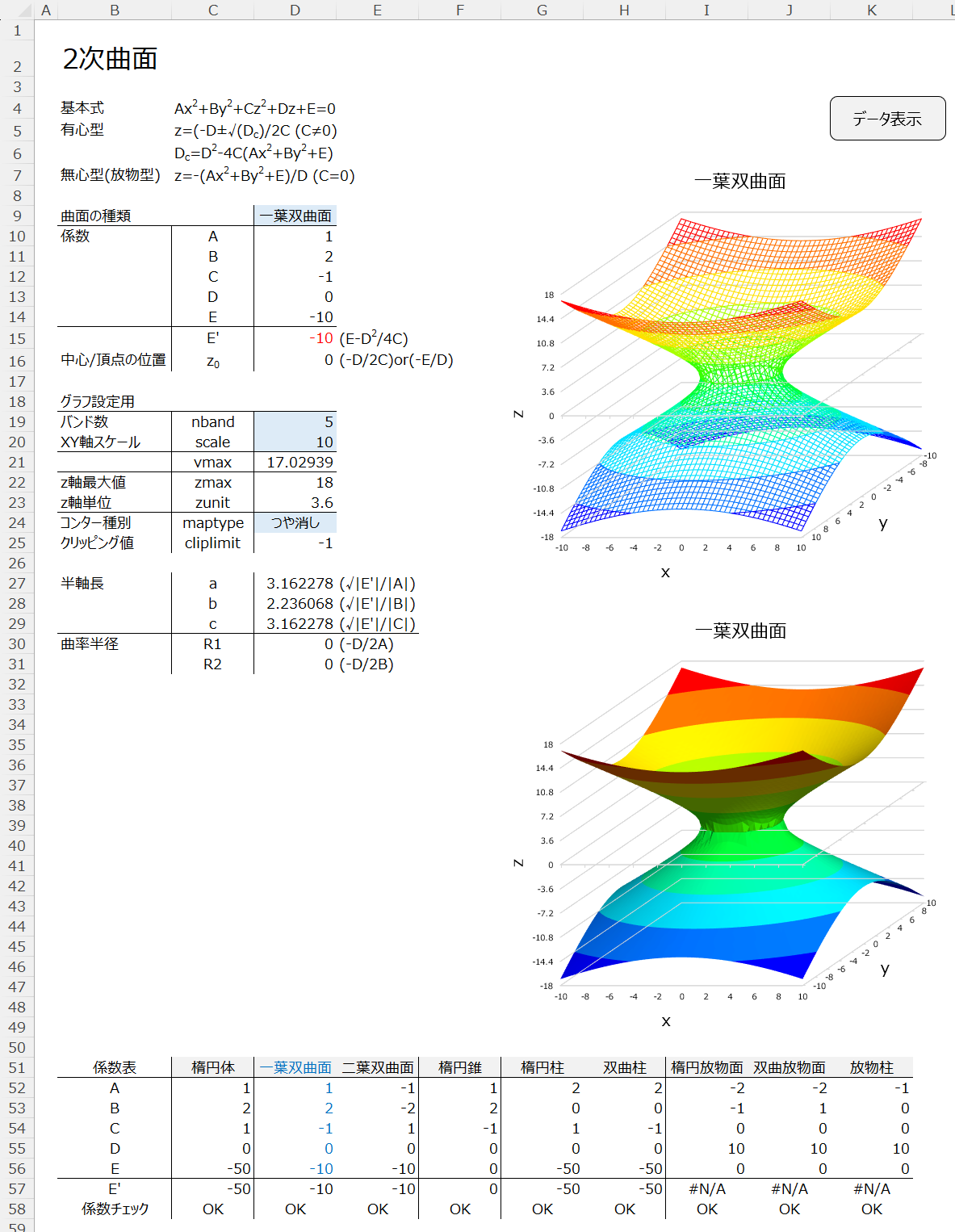
本記事で解説した式を用いて、代表的な2次曲面を描画するExcelシートです。
D9セルのプルダウンから曲面の種類を選択すると、対応した曲面の3D(等高線)グラフを表示します。
グラフは、ワイヤーフレームとコンターの2種類を描画します。
なお、グラフ生成には、本HPに掲載の等高線グラフやグラフの正方格子化のアルゴリズムに手を加えたコードを使用しています。
係数表にはサンプルデータをセットしていますが、本記事の曲面種別の係数設定ルールを参考にして*、自由に値を設定してみてください。
*) 各曲面について、簡単な係数チェックを行うようにしています。
なお動作には、Excel2021以降またはMicrosoft365の環境が必要です(revB以降)。
自学用や教育用途としてお役立てください。
2025.11.16 更新 (revB→revB1)
DL解除コード:a615
