2次曲線の一般式
928
|
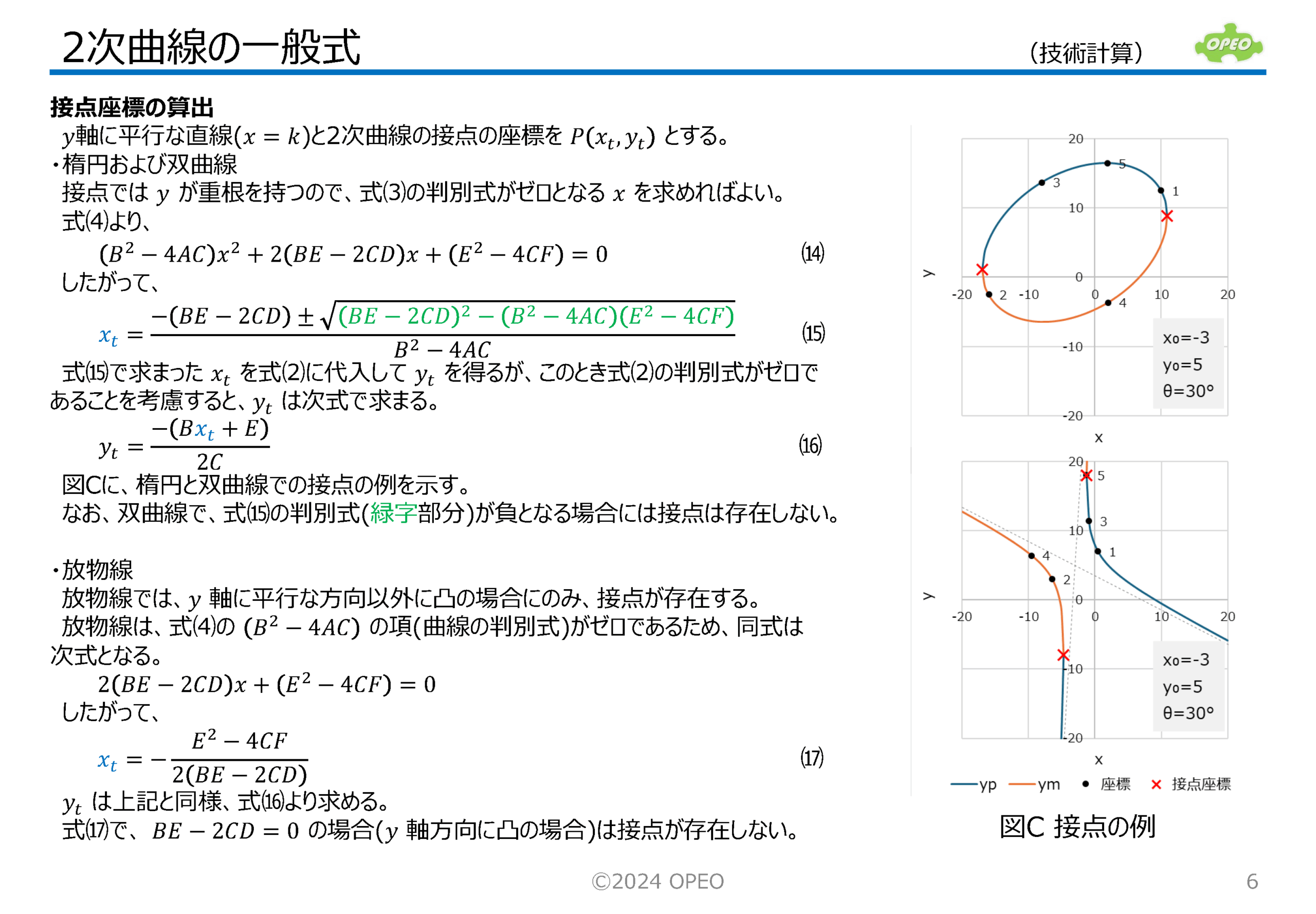
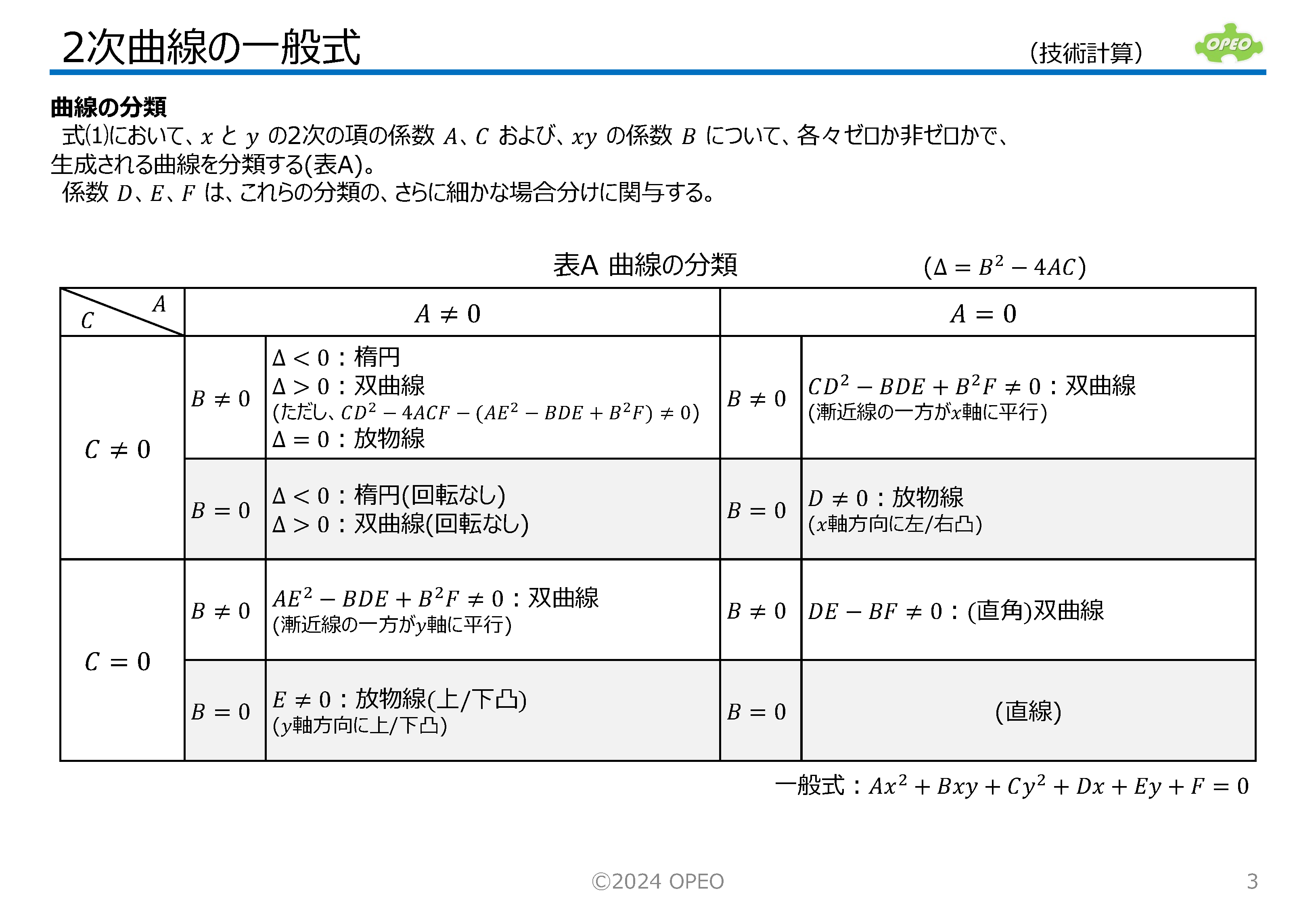
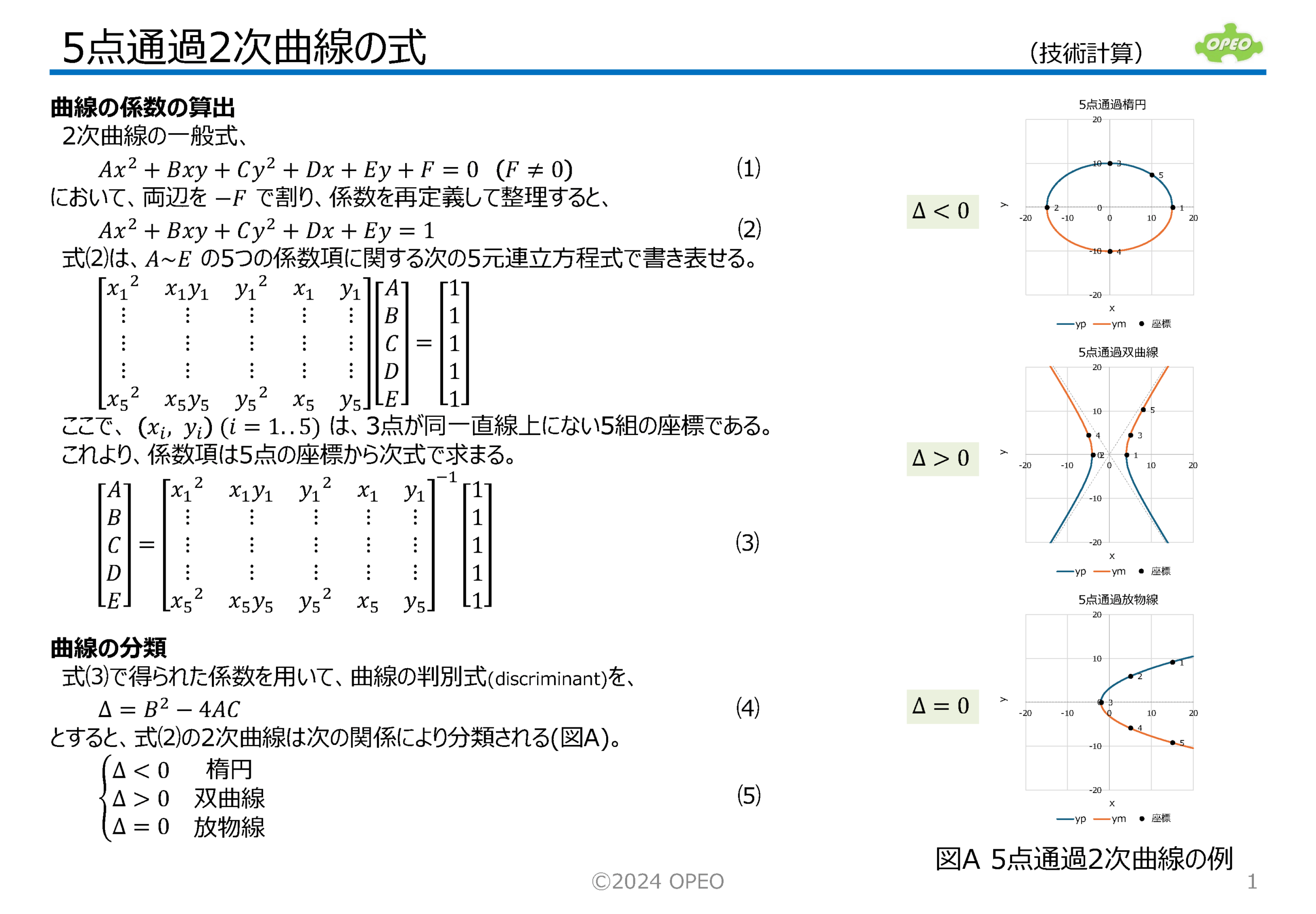
2次曲線の一般式の解説です。 2次曲線には楕円(ellipse)、双曲線(hyperbola)、放物線(parabola)がありますが、この記事では、これらの形を決めるための係数と、位置や傾きおよび接点を求める式の導出手順について説明しています (連立方程式を解く際は、Excelの行列関数を使えば簡単にできます)。 2次曲線の一般式は、 一方、係数が未知で、点の座標から2次曲線を求めるには、係数に関する方程式を立てる必要があります。 さて、右図上は一般形の楕円の例ですが、これを原点を中心とした標準形にするためには、 なお、2次曲線の一般式において、 |
|
|
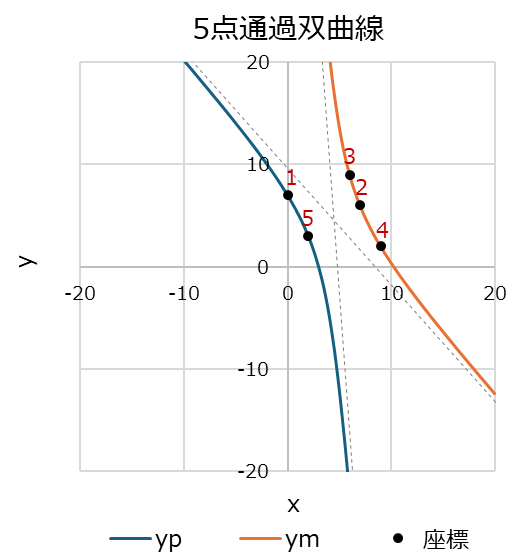
記事の終わりでは、1/7楕円と呼ばれる興味深い現象(1/7=0.142857…の循環節の数列を座標とした楕円がただ1つ決まる)についても紹介しています。 ちなみに、循環節が5桁あるいは6桁となる小数列では同様の現象があり、例えば1/7(楕円),1/13(双曲線),1/21(双曲線),1/39(楕円),1/41(双曲線),1/63(楕円),1/77(双曲線),1/91(楕円)となります。 右図下は、1/13(=0.076923…)の場合の双曲線です。 |
 |
<参考URL>
・One-Seventh Ellipse (Wolfram MathWorld)



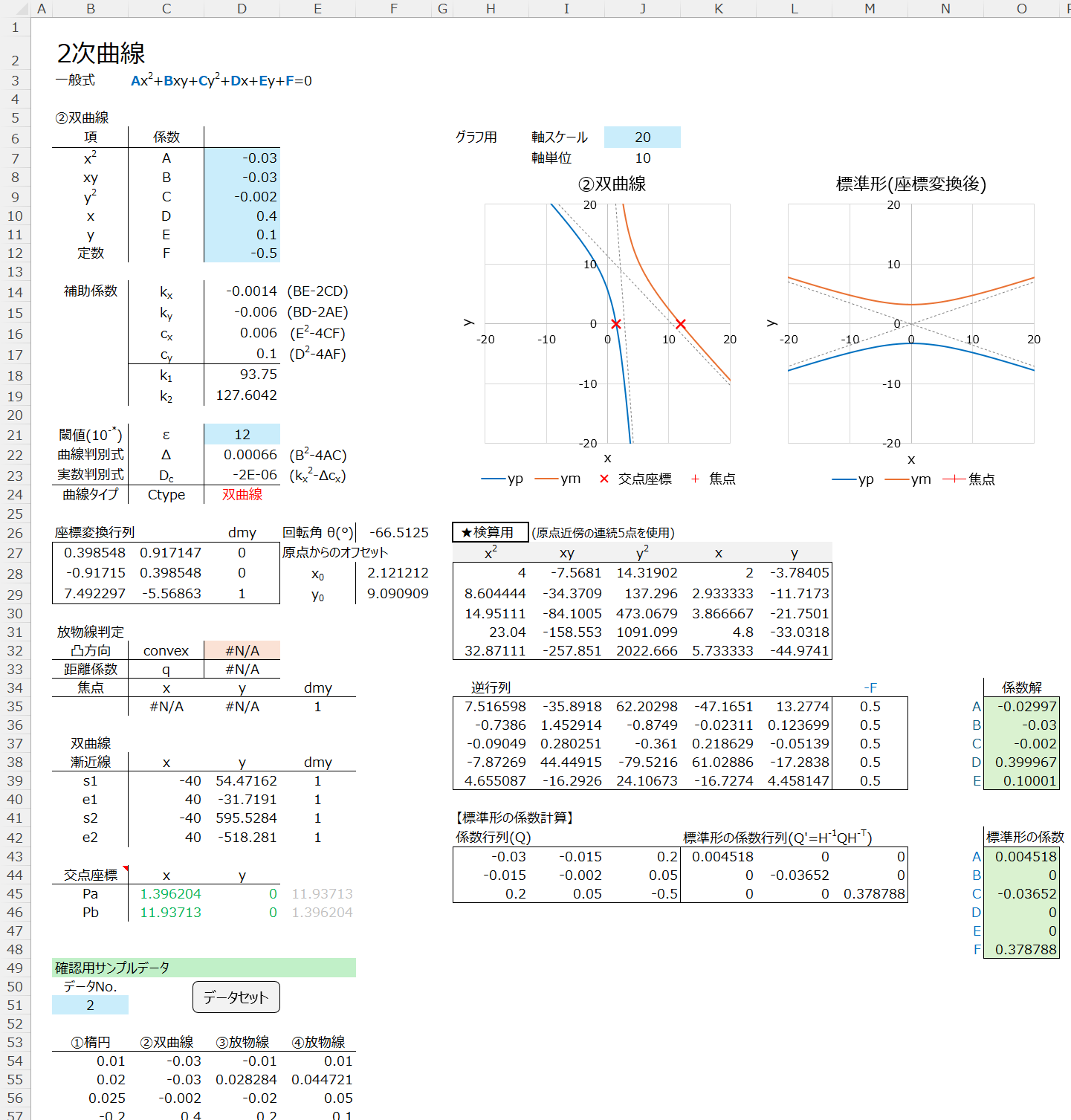
2次曲線サンプルExcel
本記事の手順を基に、2次曲線を描画するExcelのサンプルです。
係数を指定する方法と座標(5点)を指定する方法の2つのシートがあります。
各シート内に、代表的な数値データ表を用意しています。
データNo.を指定して「データセット」ボタンを押すことで、曲線が表示されます。
自学用や教育用途としてお役立てください。
<更新履歴>
・revB:データ処理方法を変更しました。
これにともない、Excel2024以降またはMicrosoft365の環境が必要となります。
2025.11.22 更新 (revA→revB)
DL解除コード:a616