シンプソン法 (数値積分法)
19,298
|
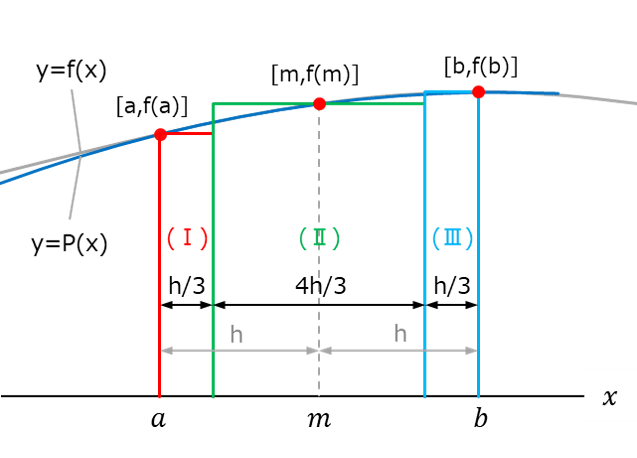
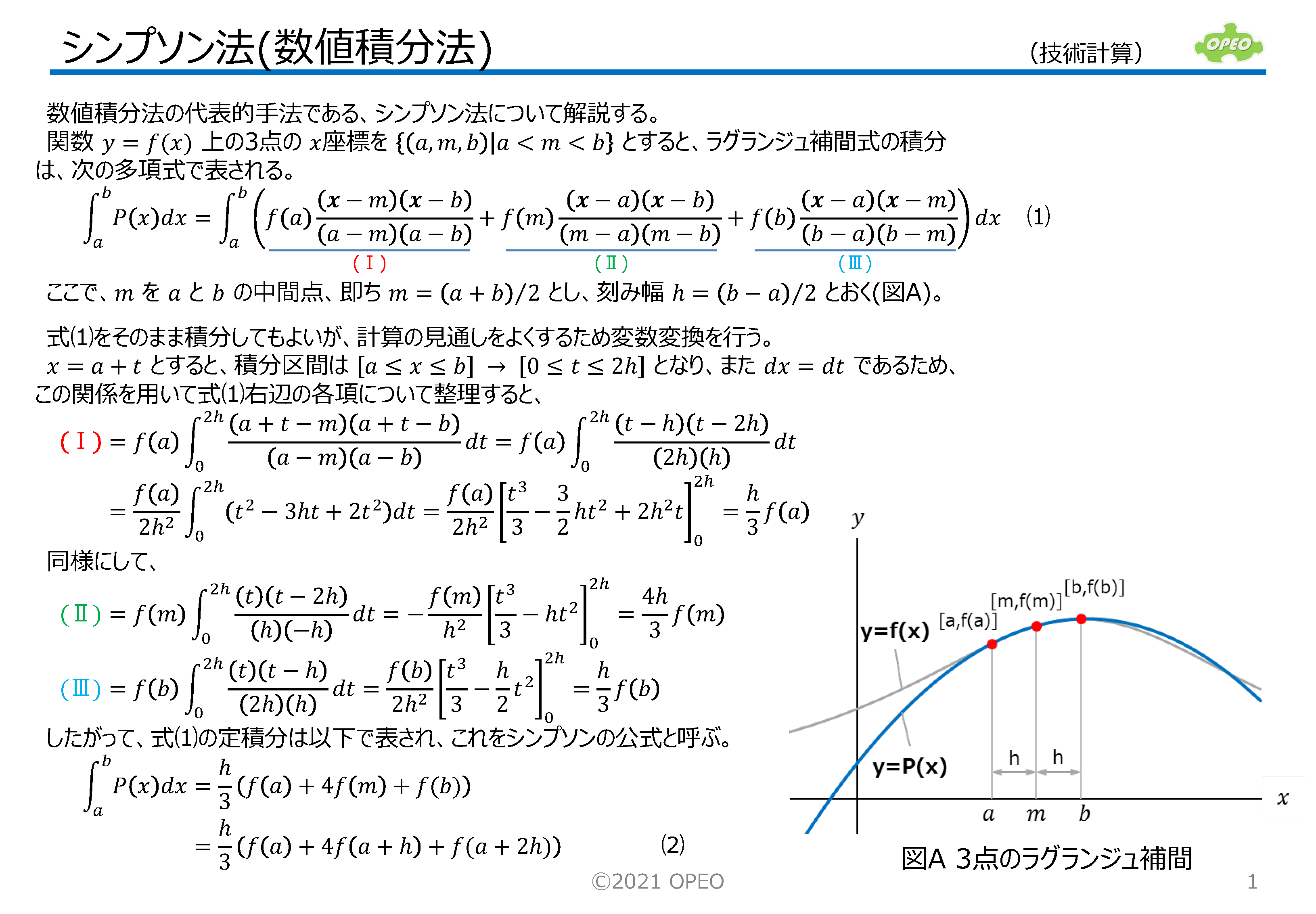
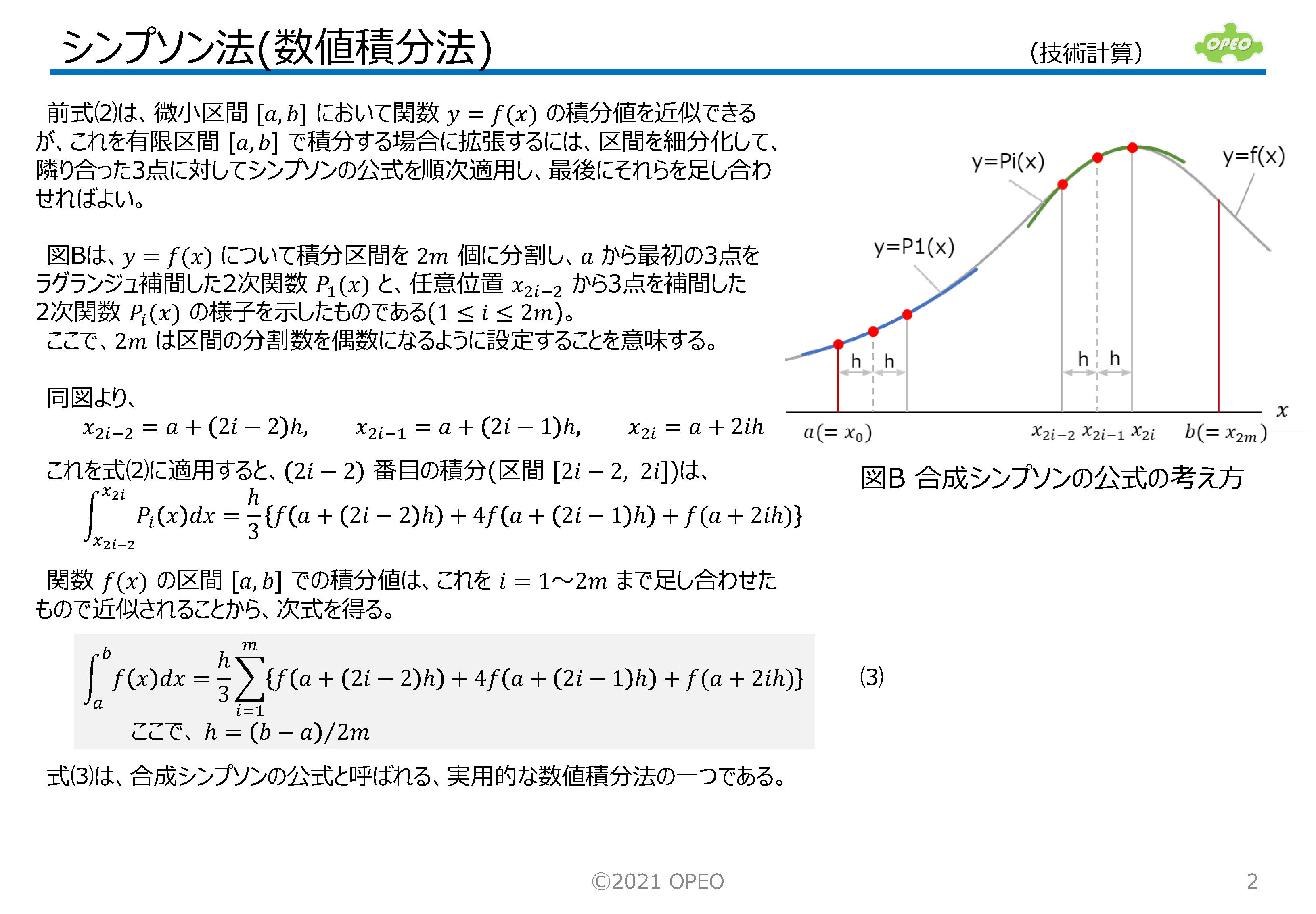
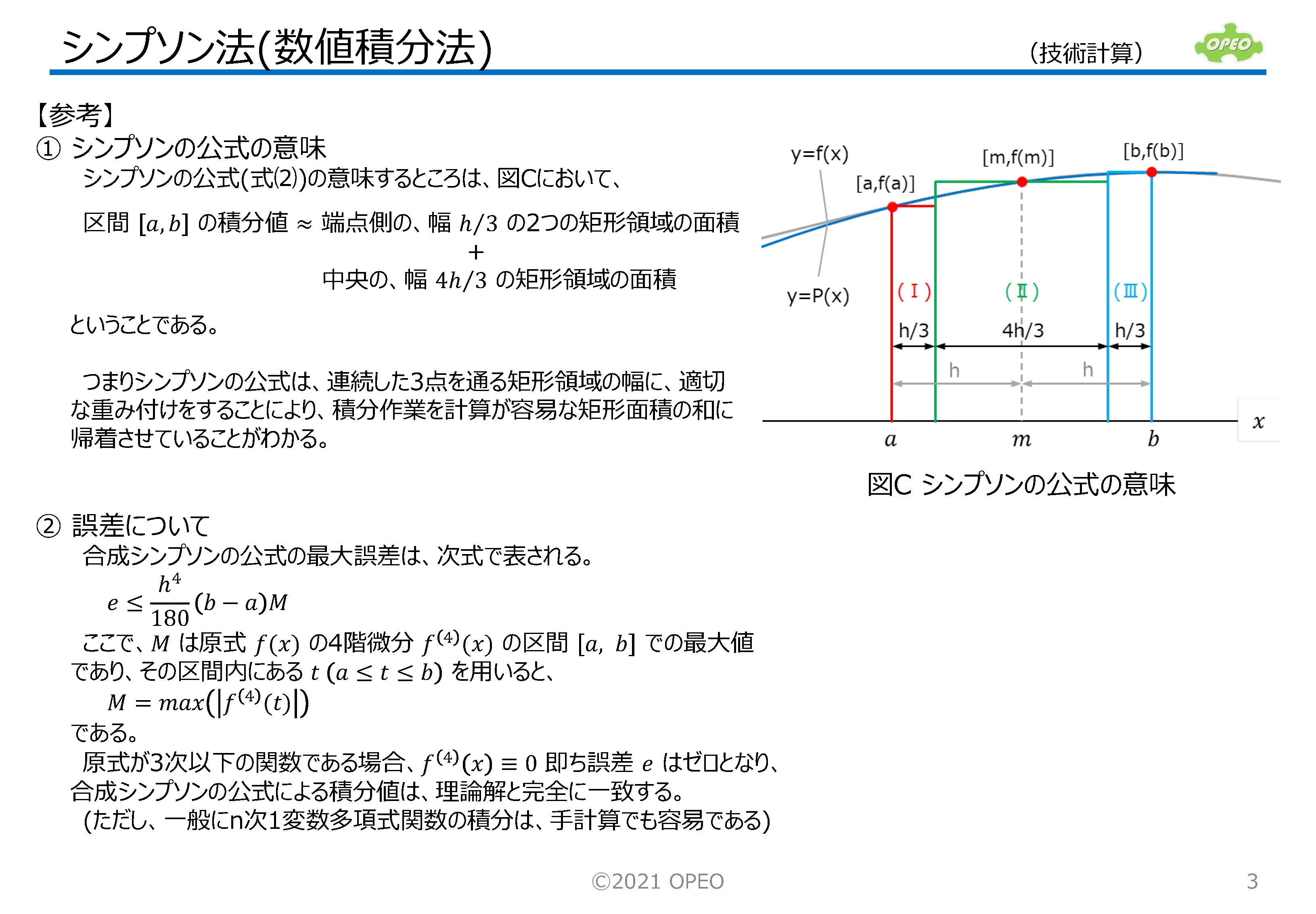
シンプソン法は、任意曲線上の3個の点を通る2次曲線を用いて、数値積分する方法です。 ラグランジュ補間は、n個の点を通る曲線を(n-1)次の多項式で近似する手法で、シンプソン法ではn=3の場合に相当します。 ここではシンプソン法の基本的な考え方と、実用的な数値積分方法である合成シンプソンの公式について解説しています。 参考として、シンプソン法を用いた計算の、Excelサンプルを掲載しています。 |
 |
<参考資料>
・山本有作(2007), ” 4.3 台形公式とシンプソン公式の誤差 “, 計算アルゴリズム講義-数値積分法(名古屋大学)
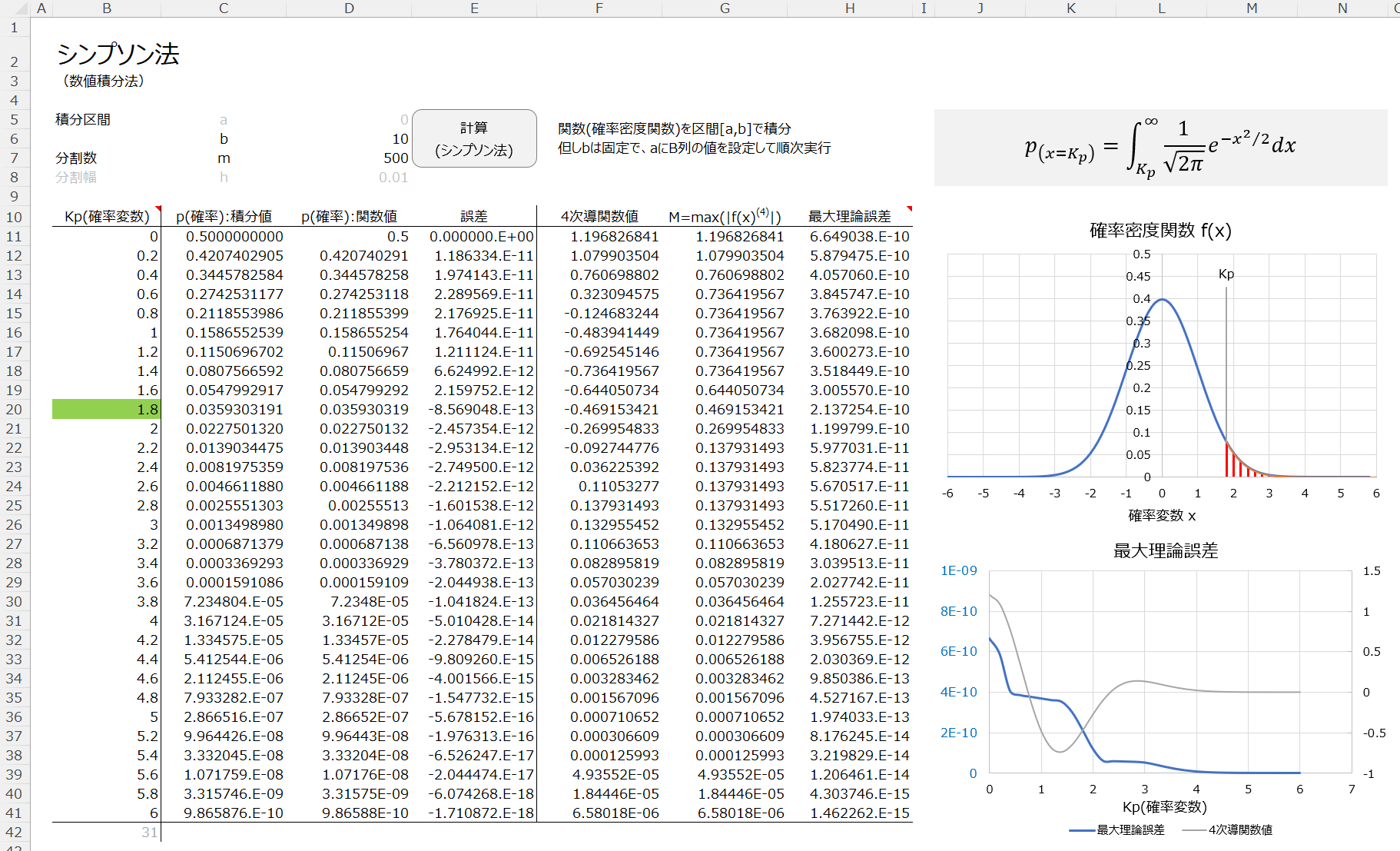
シンプソン法サンプル
このサンプルは、確率密度関数の積分値(=確率)とExcelの関数値(NORM.S.DIST)を比較したものですが、両者に殆ど実用上の差異がないことがわかります。
B列の確率変数のセルを選択すると、その数値に応じてグラフがリアルタイムに更新されます(別掲の部分領域グラフ作成手法をアレンジして使っています)。
revD以降、ActiveXに関するMicrosoftのポリシー変更に対応するため、マクロ実行ボタンの表示方法を変更しています。
2025.6.14 更新 (revC2→revD)
DL解除コード：a604
