最小二乗円
1,280
|
■最小二乗円の算出方法に関する記事です。 真円度や同軸度の測定では、真円度測定器などで円筒面の凹凸データ(測得データ)を取得して、データのばらつきを最小とする近似円を求めます。 最小二乗円の計算の基本は、回帰分析での最小二乗法になりますが、直線回帰と異なり数学的には少し複雑な手順を踏むことになります。 |
 |
|
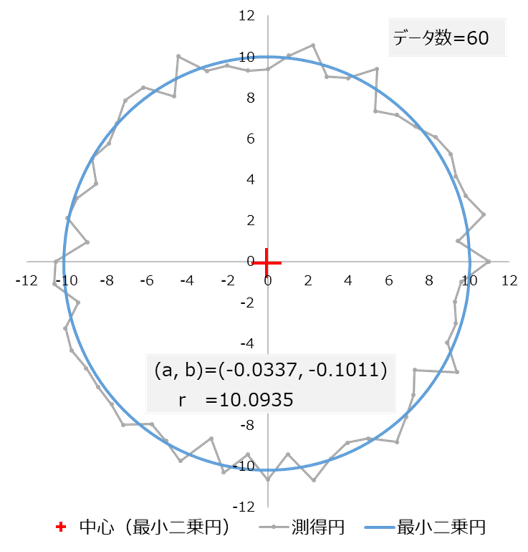
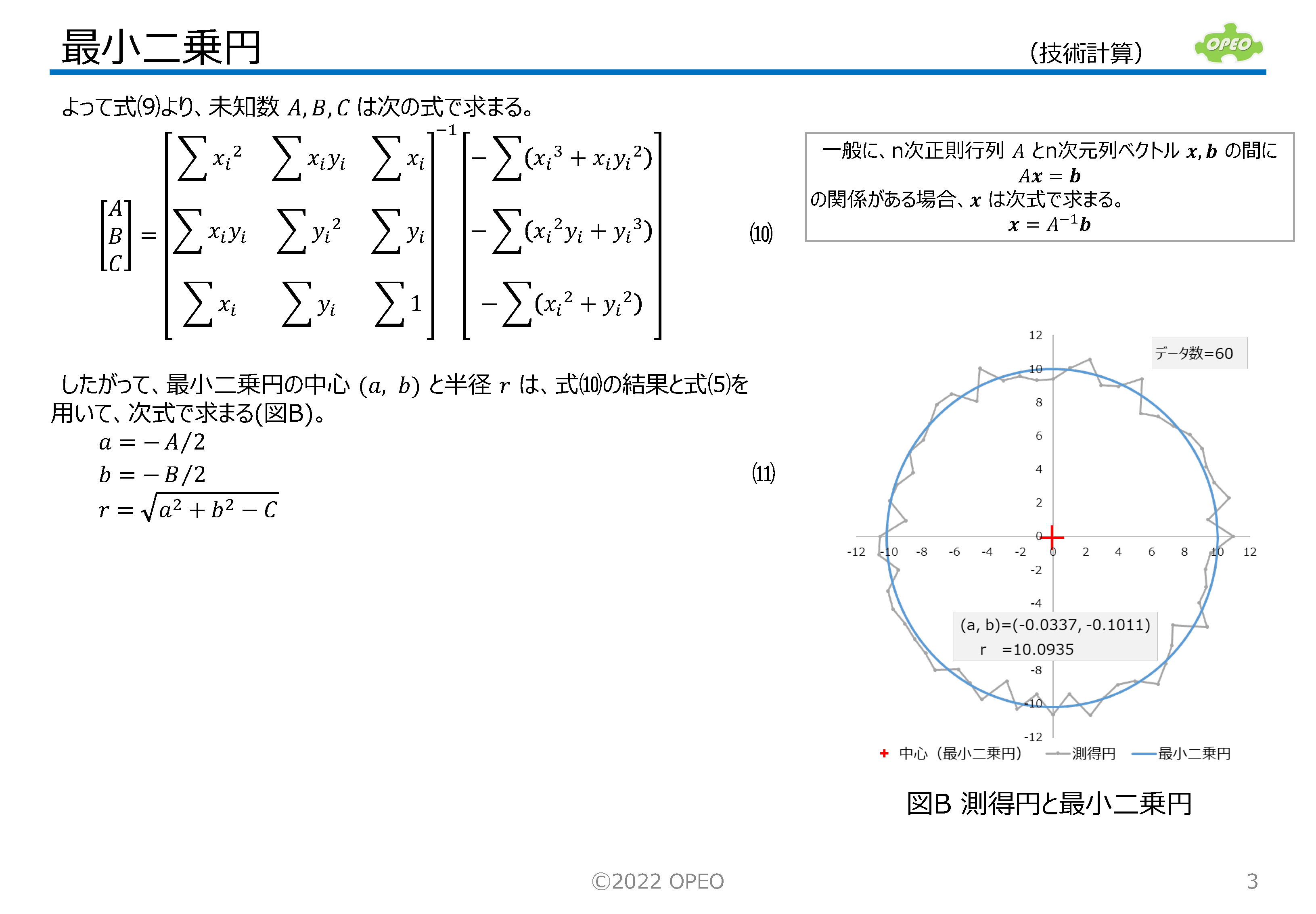
なお後半では、JIS B7451:1997 の附属書2に記載されている、最小二乗円の近似式(右欄)の導出方法について解説しています。 |
円筒面の n 個の測定データ (xn,yn) を用いると、近似円の中心座標 (a,b) と半径 R は、次式で求まる。 a = 2Σxi / n |
<参考URL>
・一般式による最小二乗法(円の最小二乗法)
<参考規格>
・JIS B7451:1997 真円度測定機
・ISO 4291-1985 Methods for the assessement of departure from roundness – Measurement of variations in radius


最小二乗円サンプル
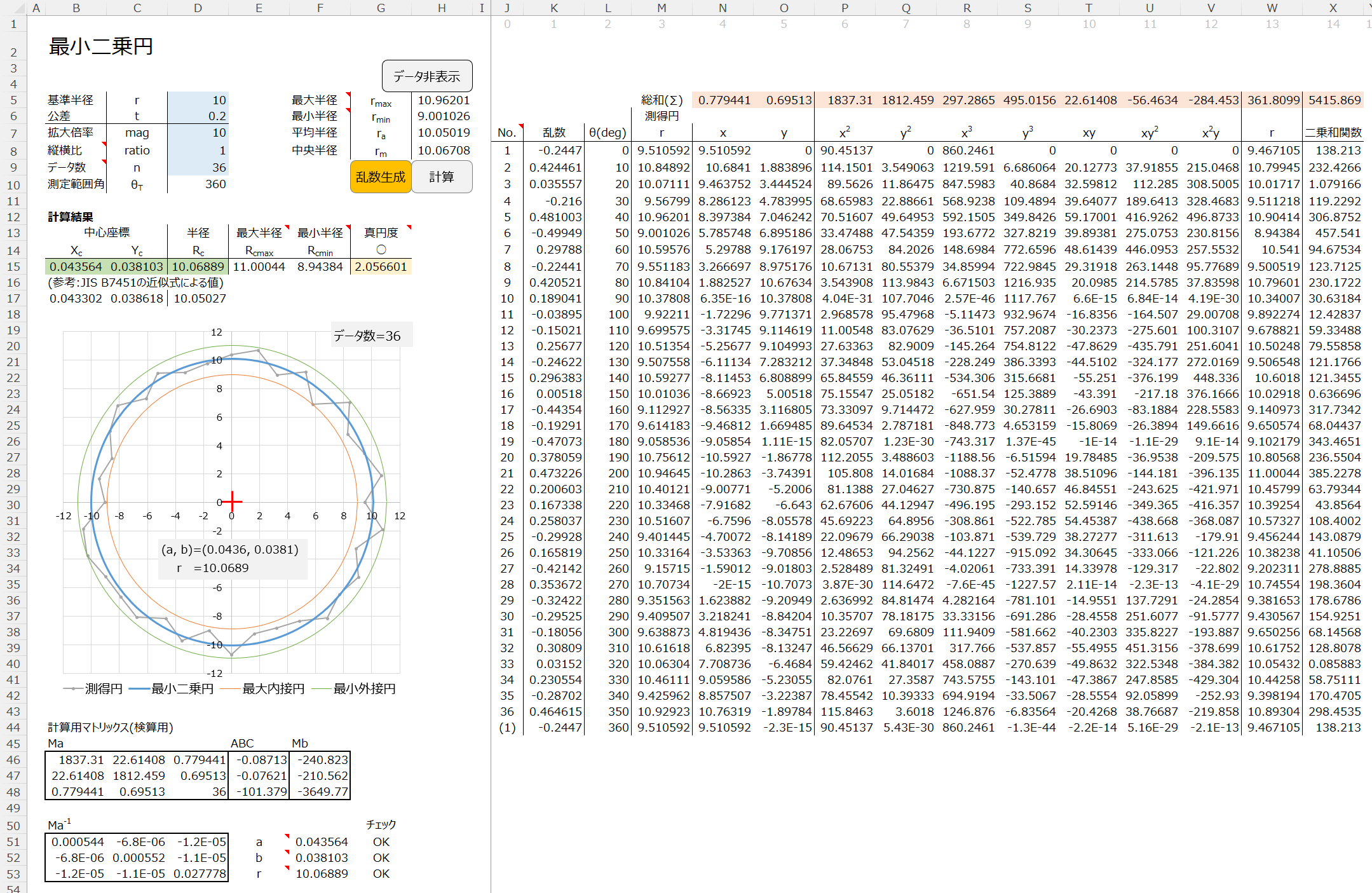
本記事で解説した手順に則って、最小二乗円を求めるExcelファイルです。
サンプル版のシートでは、乱数生成ボタンを押すと、基準半径をゼロ基準としたばらつきデータが作成され、計算が実行されます。
手動版のシートでは、x,y座標を入力後計算ボタンを押すことで、計算が実行されます。
<更新履歴>
・revD:データ処理方法を変更しました。これにより、Excel2021以降またはMicrosoft365の環境が必要となります。
2025.12.6 公開 (revD)
DL解除コード:a608