大数の法則と中心極限定理

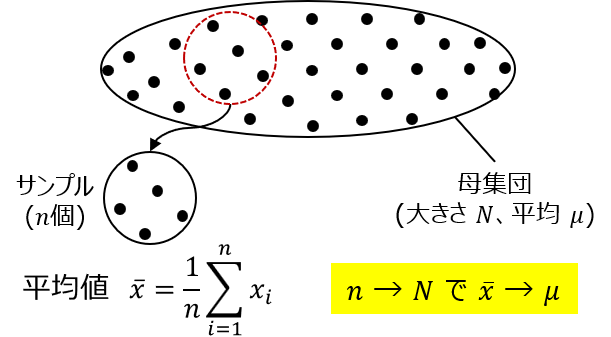
■大数の法則と中心極限定理に関する解説です。

　大数の法則と中心極限定理は、確率・統計論における基本定理であり、ばらつきが正規分布に従うとして公差計算を行うための、合理的な根拠でもあります。

　公差計算では通常、個々の部品のばらつきが正規分布に従うとして、二乗和平方根(RSS)を用います。
　これには分散の加法性が利用されていますが、それ自体は個々の確率分布の形態には依存しません。
　また記事内で説明しているように、中心極限定理は部品点数が概ね3以上であれば、これも個々の確率分布に依存しません。
　つまり一般的には、個々の部品のばらつきがどのようであっても、組立て状態でのばらつきは正規分布に従うとして公差計算を行ってよい、ということになります。